题目内容
如图,在平面直角坐标系 中,椭圆
中,椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 .
.
分别过 ,
, 的两条弦
的两条弦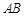 ,
, 相交于点
相交于点 (异于
(异于 ,
, 两点),且
两点),且 .
.
(1)求椭圆的方程;
(2)求证:直线 ,
, 的斜率之和为定值.
的斜率之和为定值.
(1)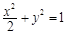 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)根据条件“右焦点为 ,离心率为
,离心率为 ”得到含有
”得到含有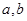 的两个方程,进而求解椭圆方程;(2)通过直线
的两个方程,进而求解椭圆方程;(2)通过直线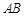 和直线
和直线 与椭圆连接方程组,得到四点坐标,统一变量,减少字母,然后利用斜率公式证明直线
与椭圆连接方程组,得到四点坐标,统一变量,减少字母,然后利用斜率公式证明直线 ,
, 的斜率之和为定值.在第(2)问的运算上要注意先化简再代入.本题的几何背景是:在如图所示的圆中,因为
的斜率之和为定值.在第(2)问的运算上要注意先化简再代入.本题的几何背景是:在如图所示的圆中,因为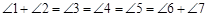 ,且
,且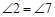 ,所以
,所以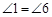 .
.
试题解析:(1)解:由题意,得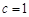 ,
,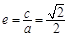 ,故
,故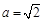 ,
,
从而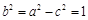 ,
,
所以椭圆的方程为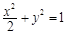 . ① 5分
. ① 5分
(2)证明:设直线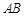 的方程为
的方程为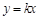 , ②
, ②
直线 的方程为
的方程为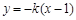 , ③ 7分
, ③ 7分
由①②得,点 ,
, 的横坐标为
的横坐标为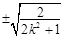 ,
,
由①③得,点 ,
, 的横坐标为
的横坐标为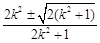 , 9分
, 9分
记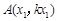 ,
,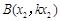 ,
,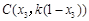 ,
,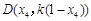 ,
,
则直线 ,
, 的斜率之和为
的斜率之和为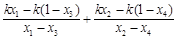
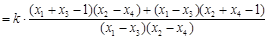
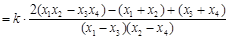 13分
13分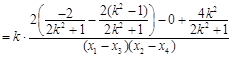
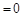 . 16分
. 16分
考点:1.椭圆的标准方程;2.直线的斜率;3.直线与椭圆的位置关系.

练习册系列答案
相关题目
已知椭圆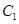 ,抛物线
,抛物线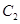 的焦点均在
的焦点均在 轴上,
轴上,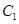 的中心和
的中心和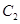 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
 |  | 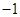 | 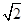 | 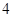 |
 | 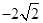 | 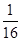 | 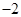 | 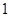 |
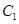 ,
,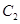 的标准方程;
的标准方程;(2)设斜率不为0的动直线
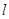 与
与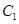 有且只有一个公共点
有且只有一个公共点 ,且与
,且与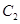 的准线交于
的准线交于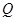 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点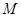 ,使得以
,使得以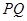 为直径的圆恒过点
为直径的圆恒过点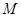 ?若存在,求出
?若存在,求出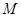 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由. 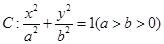 的左、右焦点分别为
的左、右焦点分别为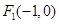 、
、 ,P为椭圆
,P为椭圆 上任意一点,且
上任意一点,且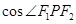 的最小值为
的最小值为 .
.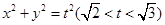 与椭圆
与椭圆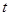 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.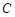 的参数方程为
的参数方程为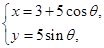
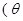 是参数
是参数 ,
,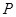 是曲线
是曲线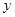 轴正半轴的交点.以坐标原点
轴正半轴的交点.以坐标原点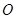 为极点,
为极点,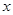 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点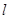 的极坐标方程.
的极坐标方程.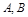 分别是椭圆
分别是椭圆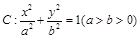 的左、右顶点,点
的左、右顶点,点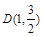 在椭圆
在椭圆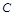 上,且直线
上,且直线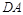 与直线
与直线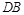 的斜率之积为
的斜率之积为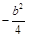 .
. 是椭圆
是椭圆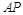 与
与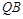 交于点
交于点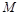 ,直线
,直线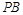 与
与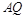 交于点
交于点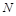 .① 求证:
.① 求证: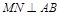 ;② 若弦
;② 若弦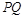 过椭圆的右焦点
过椭圆的右焦点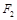 ,求直线
,求直线 的方程.
的方程.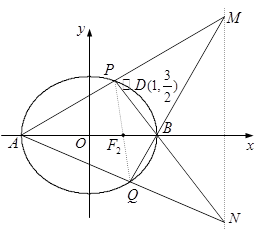
 :
:
 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,且其短轴上的一个端点到
,且其短轴上的一个端点到 的距离为
的距离为 .
. 是椭圆
是椭圆 ,使得
,使得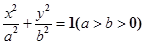 的两个顶点,
的两个顶点, 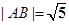 ,直线AB的斜率为
,直线AB的斜率为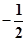 .求椭圆的方程;(2)设直线
.求椭圆的方程;(2)设直线 平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,
平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,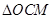 的面积等于
的面积等于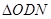 的面积.
的面积.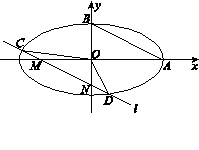
 的中心在原点,焦点在
的中心在原点,焦点在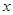 轴上,离心率
轴上,离心率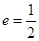 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线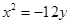 的焦点.
的焦点.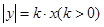 的交点为
的交点为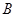 、
、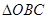 面积的最大值.
面积的最大值. 的焦距为4,且过点
的焦距为4,且过点 .
. 为椭圆
为椭圆 上一点,过点
上一点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 。取点
。取点 ,连接
,连接 ,过点
,过点 作
作 。点
。点 是点
是点 轴的对称点,作直线
轴的对称点,作直线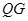 ,问这样作出的直线
,问这样作出的直线