题目内容
已知函数f(x)=x3,
(Ⅰ)记φ(x)=f(x)+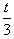 f′(x)(t∈R),求φ(x)的极小值;
f′(x)(t∈R),求φ(x)的极小值;
(Ⅱ)若函数h(x)=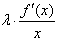 +sinx的图象上存在互相垂直的两条切线,求实数λ的值及相应的切点坐标。
+sinx的图象上存在互相垂直的两条切线,求实数λ的值及相应的切点坐标。
(Ⅰ)记φ(x)=f(x)+
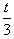 f′(x)(t∈R),求φ(x)的极小值;
f′(x)(t∈R),求φ(x)的极小值;(Ⅱ)若函数h(x)=
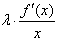 +sinx的图象上存在互相垂直的两条切线,求实数λ的值及相应的切点坐标。
+sinx的图象上存在互相垂直的两条切线,求实数λ的值及相应的切点坐标。解:(Ⅰ)由已知: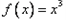 ,
,
∴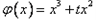 ,
,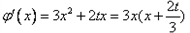 ,
,
由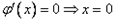 ,或
,或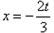 ,
,
当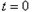 时,
时,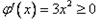 ,
,
∴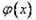 在
在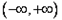 为增函数,此时不存在极值;
为增函数,此时不存在极值;
当t>0时,x变化时,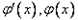 变化如下:
变化如下:
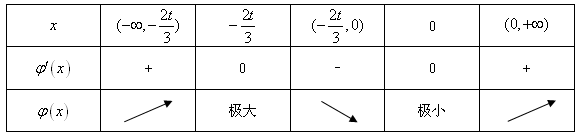
由上表可知: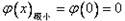 ;
;
当t<0时,x变化时, 变化如下:
变化如下:
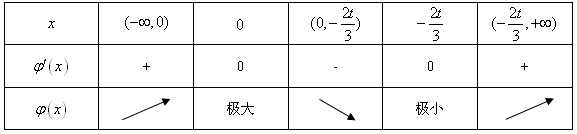
由上表可知: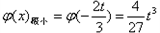 。
。
(Ⅱ)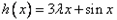
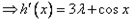 ,
,
设两切点分别为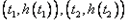 ,
,
则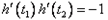 ,
,
即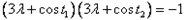
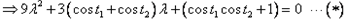 ,
,
∵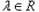 ,
,
∴方程(*)的判别式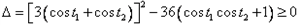 ,
,
即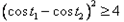 ,
,
又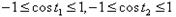 ,
,
∴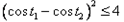 ,
,
从而可得: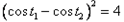 ,
,
上式要成立当且仅当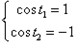 或
或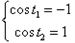 ,
,
此时方程(*)的解为λ=0,
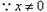 ,
,
∴存在λ=0,此时函数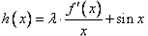 的图象在点
的图象在点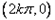
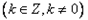 处的切线和在点
处的切线和在点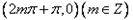 处的切线互相垂直。
处的切线互相垂直。
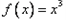 ,
,∴
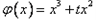 ,
,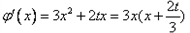 ,
,由
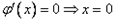 ,或
,或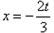 ,
,当
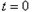 时,
时,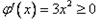 ,
,∴
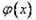 在
在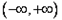 为增函数,此时不存在极值;
为增函数,此时不存在极值;当t>0时,x变化时,
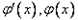 变化如下:
变化如下:
由上表可知:
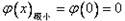 ;
;当t<0时,x变化时,
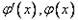 变化如下:
变化如下:
由上表可知:
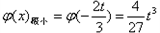 。
。(Ⅱ)
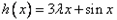
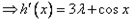 ,
,设两切点分别为
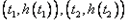 ,
,则
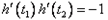 ,
,即
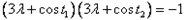
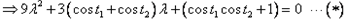 ,
,∵
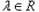 ,
,∴方程(*)的判别式
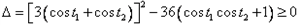 ,
,即
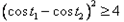 ,
,又
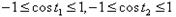 ,
,∴
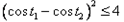 ,
,从而可得:
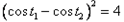 ,
,上式要成立当且仅当
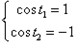 或
或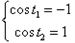 ,
,此时方程(*)的解为λ=0,
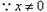 ,
,∴存在λ=0,此时函数
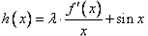 的图象在点
的图象在点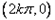
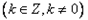 处的切线和在点
处的切线和在点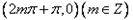 处的切线互相垂直。
处的切线互相垂直。 
练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|