题目内容
已知数列 {an} 的前 n 项和 Sn=32n-n2 ,求数列 {|an|} 的前n项和Tn.
解:当n≥2时,an=Sn-Sn-1=(32n-n2)-[32(n-1)-(n-1)2]=33-2n.
又a1=S1=31 适合上式,
∴an=33-2n.
由an=33-2n≥0得n≤![]() =16.5.所以等差数列{an}中前16项为正数项,从第17项开始,各项为负数,
=16.5.所以等差数列{an}中前16项为正数项,从第17项开始,各项为负数,
因此:
当0<n≤16时,Tn=Sn=32-n2,
当n≥17时,
Tn=S16-(a17+a18+a19+…+an)=2S16-Sn
=-(32-n2)+2(32 × 16-162)
=n2-32n+512.
综上所述,
∴Tn=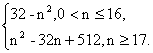

练习册系列答案
相关题目