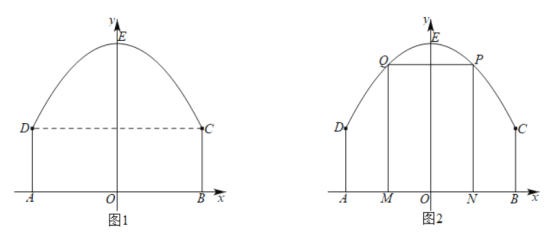题目内容
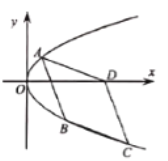
【题目】已知椭圆![]() 的标准方程是
的标准方程是![]() ,设
,设![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 做
做![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() ,
,![]() .
.
(1)证明:线段![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(2)当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
【答案】(1)证明见解析;(2)![]() 或
或![]() .
.
【解析】
(1)由椭圆的标准方程可得![]() 的坐标,设
的坐标,设![]() 点坐标为
点坐标为![]() ,可得直线
,可得直线![]() 的斜率,讨论
的斜率,讨论![]() 与
与![]() 两种情况,设直线
两种情况,设直线![]() 的方程是
的方程是![]() ,
,![]() ,
,![]() ;联立直线与椭圆方程,即可用
;联立直线与椭圆方程,即可用![]() 表示点
表示点![]() 的坐标,即可证明结论.
的坐标,即可证明结论.
(2)由(1)结合弦长公式,表示出![]() ,即可得
,即可得![]() ,结合基本不等式即可求得最小值及最小值时
,结合基本不等式即可求得最小值及最小值时![]() 的值,进而得点
的值,进而得点![]() 的坐标.
的坐标.
(1)证明:椭圆![]() 的标准方程是
的标准方程是![]() ,
,
设![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,
上任意一点,
所以![]() 得坐标为
得坐标为![]() ,设
,设![]() 点坐标为
点坐标为![]() ,
,
则直线![]() 的斜率
的斜率![]() ,
,
当![]() 时,直线
时,直线![]() 的斜率
的斜率![]() ,
,
直线![]() 的方程是
的方程是![]() ,
,
当![]() 时,直线
时,直线![]() 的方程
的方程![]() ,
,
也符合方程![]() 的形式,
的形式,
设![]() ,
,![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立得:
的方程联立得:
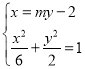 消去
消去![]() 得
得![]() ,
,
有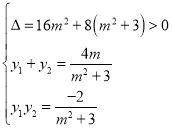 ,
,
设![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
, ![]() ,
,
所以直线![]() 的斜率
的斜率![]() ,又因为直线
,又因为直线![]() 的斜率
的斜率![]() ,
,
所以点![]() 在直线
在直线![]() 上,因此线段
上,因此线段![]() 平分线段
平分线段![]() .
.
(2)由(1)知![]() ,
,![]() ,
,
所以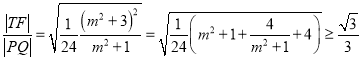 ,
,
当且仅当![]() ,
,
即![]() 时等号成立,此时
时等号成立,此时![]() 取得最小值,
取得最小值,
![]() 点的坐标为
点的坐标为![]() 或
或![]()

练习册系列答案
相关题目
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.