题目内容
【题目】（本题满分15分）如图，在半径为
的半圆形（O为圆心）铁皮上截取一块矩形材料ABCD，其中点A、B在直径上，点C、D在圆周上，将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），记圆柱形罐子的体积为
．
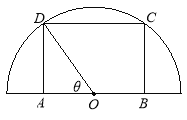
（1）按下列要求建立函数关系式：
①设
，将
表示为
的函数；
②设
（
），将表示为
的函数；
（2）请您选用（1）问中的一个函数关系，求圆柱形罐子的最大体积．
【答案】（1）①
，（
）
②
，（
）
（2）
【解析】
试题（1）要将实际问题转化为函数问题，根据题意构建数学模型，利用直角三角形
求底面圆的半径
，进而列出函数关系式（2）求体积的最大值转化为求函数的最大值，先求导，再判断单调性，再求最值。
试题解析：解：（1）①
，
，
，（） 4分
②
，
，
，（） 8分
（2）选用
：
，
，
令
，则
10分
列表得：
|
|
|
|
|
|
|
|
| 单调增 | 极大值 | 单调减 |
（不列表，利用导函数的符号，判断出单调性同样得分）
选用
：令
，
，
令 
，则
10分
列表得：
|
|
|
|
|
|
|
|
| 单调增 | 极大值 | 单调减 |
，即
15分
（对
直接求导求解也得分，
）
答：圆柱形罐子的最大体积为．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
