题目内容
20.在数列{an}中,a1=$\frac{5}{3}$,且3an+1=an+2.(1)设bn=an-1,证明:数列{bn}是等比数列,并求出{an}的通项公项;
(2)设${c_n}=log_3^{\frac{{{{({a_n}-1)}^2}}}{4}}$,数列$\left\{{\frac{1}{{{c_n}{c_{n+2}}}}}\right\}$的前n项和为Tn,是否存在最小的正整数m,使得对于任意的n∈N*,均有Tn<$\frac{m}{16}$成立,若存在,求出m的值,若不存在,请说明理由.
分析 (1)由题意可得3(an+1-1)=(an-1),从而可得b1=$\frac{2}{3}$,$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{1}{3}$,从而证明;从而求得an=$\frac{2}{3}$•$(\frac{1}{3})^{n-1}$+1;
(2)化简${c_n}=log_3^{\frac{{{{({a_n}-1)}^2}}}{4}}$=log3$\frac{(\frac{2}{3}•(\frac{1}{3})^{n-1})^{2}}{4}$=log33-2n=-2n,从而可得$\frac{1}{{c}_{n}{c}_{n+2}}$=$\frac{1}{8}$($\frac{1}{n}$-$\frac{1}{n+2}$),从而利用裂项求和法求解.
解答 解:(1)∵3an+1=an+2,∴3(an+1-1)=(an-1),
又∵b1=a1-1=$\frac{5}{3}$-1=$\frac{2}{3}$,∴$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{a}_{n+1}-1}{{a}_{n}-1}$=$\frac{1}{3}$,
故数列{bn}是以$\frac{2}{3}$为首项,$\frac{1}{3}$为公比的等比数列;
∴bn=an-1=$\frac{2}{3}$•$(\frac{1}{3})^{n-1}$,
∴an=$\frac{2}{3}$•$(\frac{1}{3})^{n-1}$+1;
(2)${c_n}=log_3^{\frac{{{{({a_n}-1)}^2}}}{4}}$=log3$\frac{(\frac{2}{3}•(\frac{1}{3})^{n-1})^{2}}{4}$=log33-2n=-2n,
∴$\frac{1}{{c}_{n}{c}_{n+2}}$=$\frac{1}{(-2n)(-2(n+2))}$=$\frac{1}{4}$•$\frac{1}{n(n+2)}$=$\frac{1}{8}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴Tn=$\frac{1}{8}$[(1-$\frac{1}{3}$)+($\frac{1}{2}$-$\frac{1}{4}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{n-1}$-$\frac{1}{n+1}$)+($\frac{1}{n}$-$\frac{1}{n+2}$)]
=$\frac{1}{8}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{3}{16}$-$\frac{1}{8}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)<$\frac{3}{16}$,
故m≥3,
故m=3.
点评 本题考查了等比数列的证明及裂项求和法的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案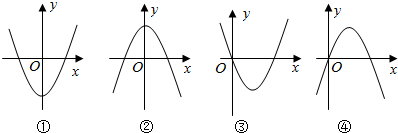 下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)=( )
下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)=( )| A. | $\frac{5}{3}$或$-\frac{1}{3}$ | B. | $\frac{5}{3}$或$\frac{1}{3}$ | C. | $-\frac{1}{3}$或$-\frac{5}{3}$ | D. | $\frac{1}{3}$或$-\frac{5}{3}$ |
| A. | c≤1 | B. | c≥1 | C. | c<0 | D. | c∈R |
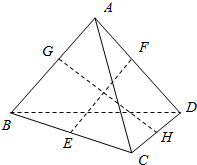 已知:正四面体ABCD(所有棱长均相等)的棱长为1,E、F、G、H分别是四面体ABCD中各棱的中点,设:$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b,\overrightarrow{AD}=\overrightarrow c$,试采用向量法解决下列问题
已知:正四面体ABCD(所有棱长均相等)的棱长为1,E、F、G、H分别是四面体ABCD中各棱的中点,设:$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b,\overrightarrow{AD}=\overrightarrow c$,试采用向量法解决下列问题