题目内容
设定义在R上的奇函数f（x）满足，对任意x1，x2∈（0，+∞），且x1≠x2都有
＜0，且f（2）=0，则不等式
≤0的解集为（ ）
| f(x1)-f(x2) |
| x2-x1 |
| 3f(-x)-2f(x) |
| 5x |
分析：由题意可得，函数的图象关于原点对称，函数在（0，+∞）上是增函数，函数在（-∞，0）上也是增函数．由不等式
≤0 可得
≥0，再由f（2）=-f（-2）=0，数形结合可得不等式的解集．
| 3f(-x)-2f(x) |
| 5x |
| f(x) |
| x |
解答：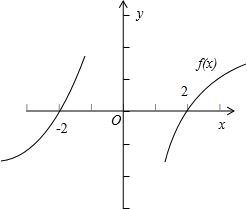
解：由题意可得，函数的图象关于原点对称，对任意x1，x2∈（0，+∞），且x1≠x2 ，
都有图象上任意两点连线的斜率k=
＞0，故函数在（0，+∞）上是增函数，
故函数在（-∞，0）上也是增函数．
由不等式
≤0 可得
≤0，
≥0．
再由f（2）=0可得f（-2）=0，故有不等式结合图象可得x≥2，或 x≤-2，
故选C．
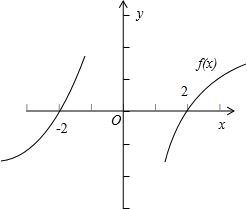解：由题意可得，函数的图象关于原点对称，对任意x1，x2∈（0，+∞），且x1≠x2 ，都有图象上任意两点连线的斜率k=
| f(x2)-f(x1) |
| x2-x1 |
故函数在（-∞，0）上也是增函数．
由不等式
| 3f(-x)-2f(x) |
| 5x |
| -5f(x) |
| 5x |
| f(x) |
| x |
再由f（2）=0可得f（-2）=0，故有不等式结合图象可得x≥2，或 x≤-2，
故选C．
点评：本题主要考查函数的单调性和奇偶性的综合应用，其它不等式的解法，体现了转化的数学思想，属于中档题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目