题目内容
已知椭圆C: 的离心率为
的离心率为 ,B,F分别是它的上顶点和右焦点.椭圆C上的点到点F的最短距离为2.圆M是过点B,F的所有圆中面积最小的圆.
,B,F分别是它的上顶点和右焦点.椭圆C上的点到点F的最短距离为2.圆M是过点B,F的所有圆中面积最小的圆.(1)求椭圆C和圆M的方程;
(2)从圆外一点P引圆M的切线PQ,切点为Q,且有|PQ|=|PO|,O是坐标原点,求|PF|的最小值.
【答案】分析:(1)直接利用条件得到关于a,c的方程,解出a,c的值即可求出椭圆C的方程;再利用过B,F的所有圆中,以BF为直径的圆面积最小,求出对应圆M的方程;
(2)先利用条件求得点P在直线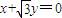 上,再把|PF|的最小值转化为点F到直线
上,再把|PF|的最小值转化为点F到直线 的距离即可.
的距离即可.
解答:解:(1)依题意有: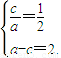 (2分)
(2分)
解得a=4,c=2.得b2=12.
所以椭圆C的方程为: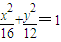 .(4分)
.(4分)
B(0,2 ),F(0,2),过B,F的所有圆中,
),F(0,2),过B,F的所有圆中,
以BF为直径的圆面积最小,
所以圆M的方程为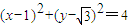 .(7分)
.(7分)
(2)设P(x1,y1),
则|PQ|2=|PM|2-R2= ,|PQ|2=x12+y12.
,|PQ|2=x12+y12.
因为|PQ|=|PO|,得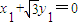 .(10分)
.(10分)
所以点P在直线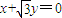 上,
上,
故|PF|的最小值即为点F到直线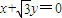 的距离(12分)
的距离(12分)
故|PF|的最小值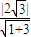 =
=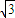 .(14分)
.(14分)
点评:本题是对圆和椭圆的综合考查.在做这一类型题时,一定要认真读题,理解题意.
(2)先利用条件求得点P在直线
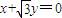 上,再把|PF|的最小值转化为点F到直线
上,再把|PF|的最小值转化为点F到直线 的距离即可.
的距离即可.解答:解:(1)依题意有:
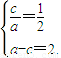 (2分)
(2分)解得a=4,c=2.得b2=12.
所以椭圆C的方程为:
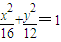 .(4分)
.(4分)B(0,2
 ),F(0,2),过B,F的所有圆中,
),F(0,2),过B,F的所有圆中,以BF为直径的圆面积最小,
所以圆M的方程为
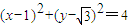 .(7分)
.(7分)(2)设P(x1,y1),
则|PQ|2=|PM|2-R2=
 ,|PQ|2=x12+y12.
,|PQ|2=x12+y12.因为|PQ|=|PO|,得
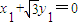 .(10分)
.(10分)所以点P在直线
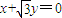 上,
上,故|PF|的最小值即为点F到直线
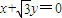 的距离(12分)
的距离(12分)故|PF|的最小值
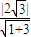 =
=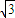 .(14分)
.(14分)点评:本题是对圆和椭圆的综合考查.在做这一类型题时,一定要认真读题,理解题意.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.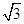
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线