题目内容
判断下列各函数的奇偶性:(1)f(x)=(x-1)
|
(2)f(x)=
| lg(1-x2) |
| |x2-2|-2 |
(3)f(x)=
|
分析:主要考查函数的奇偶性判断的步骤:①求定义域②定义域是否关于原点对称③化简解析式后判断f(-x)与f(x)的关系④得出结论
解答:解:(1)由
≥0,得定义域为[-1,1),
关于原点不对称,∴f(x)为非奇非偶函数.
(2)由
得定义域为(-1,0)∪(0,1),
∴f(x)=
=-
,
∵f(-x)=-
=-
=f(x)
∴f(x)为偶函数
(3)当x<0时,-x>0,则f(-x)=-(-x)2-x=-(x2+x)=-f(x),
当x>0时,-x<0,则f(-x)=(-x)2-x=-(-x2+x)=-f(x),
综上所述,对任意的x∈(-∞,+∞),都有f(-x)=-f(x),∴f(x)为奇函数.
| 1+x |
| 1-x |
关于原点不对称,∴f(x)为非奇非偶函数.
(2)由
|
∴f(x)=
| lg(1-x2) |
| -(x2-2)-2 |
| lg(1-x2) |
| x2 |
∵f(-x)=-
| lg[1-(-x)2] |
| (-x)2 |
| lg(1-x2) |
| x2 |
∴f(x)为偶函数
(3)当x<0时,-x>0,则f(-x)=-(-x)2-x=-(x2+x)=-f(x),
当x>0时,-x<0,则f(-x)=(-x)2-x=-(-x2+x)=-f(x),
综上所述,对任意的x∈(-∞,+∞),都有f(-x)=-f(x),∴f(x)为奇函数.
点评:对于分段函数奇偶性的判断,需特别注意x与-x所满足的对应关系,即判断x>0时f(-x)与f(x)的关系,也要判断x<0时f(-x)与f(x)的关系.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

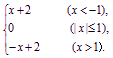
 ;
; ;
;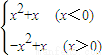 .
.