Question

判断函数f（x）=－x³＋1在（－∞，0）上是增函数还是减函数，并证明你的判断；如果x∈（0，＋∞），函数f（x）是增函数还是减函数?

Answer 1

解析： 本题考查利用函数单调性的定义证明函数的单调性.一般地，若k＞0，f（x）与kf（x）具有一致的单调性；若k＜0，则f（x）与kf（x）的单调性相反；f（x）与f（x）+b具有一致的单调性.从f（x）=－x³＋1?上可直接得出f（x）是减函数，用单调性的定义证明，应注意对差式的变形及分解因式.

答案：  f（x）=－x³＋1在（－∞，0）上是减函数，证明如下：

在（－∞，0）上任取x₁、x₂，且x₁＜x₂.

∵f（x₁）－f（x₂）=（－x₁³＋1）－（－x₂³＋1）=（x₂－x₁）（x₂²＋x₁x₂＋x₁²）=（x₂－x₁）［（x₂+）²+x₁²］，?

又x₂－x₁＞0，（x₂+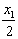）²+x₁²＞0，?

∴f（x₁）－f（x₂）＞0，即f（x₁）＞f（x₂）.?

故f（x）=－x³＋1在（－∞，0）上是减函数.?

同理，可证当x∈（0，＋∞）时，函数f（x）仍然是减函数.