题目内容

g（x）=x（2-x）的递增区间依次是（）

A.(-∞，0]，(-∞,1] B.(-∞，0]，［1，+∞)

C.［0，+∞)，(-∞，-1] D.［0，+∞］，［1，+∞］

解析：由于f(x)=|x|=g(x)=-(x-1)²+1，结合图象易知选C.

答案：C

练习册系列答案

第三学期寒假衔接系列答案

骄子之路寒假作业河北人民出版社系列答案

冬之卷快乐假日系列答案

动力源期末寒假作业系列答案

非常完美完美假期寒假作业系列答案

新浪书业复习总动员学期总复习寒系列答案

寒假大串联黄山书社系列答案

自主假期作业本吉林大学出版社系列答案

高中新课程寒假作业系列答案

海淀黄冈寒假作业合肥工业大学出版社系列答案

相关题目

设函数f（x），g（x）的定义域分别为F、G，且F、G．若对任意的x∈F，都有g（x）=f（x），则称g（x）为f（x）在G上的一个“延拓函数”．已知函数f（x）=2^x（x≤0），若g（x）为f（x）在R上一个延拓函数，且g（x）是偶函数，则函数g（x）的解析式是（　　）

A、g（x）=2^|x|

B、g（x）=log₂|x|

下列命题中：
①函数f(x)=x+

(x∈(0，1))的最小值是2

；
②对于任意实数x，有f（-x）=-f（x），g（-x）=g（x）且x＞0时，f′（x）＞0，g′（x）＞0，则x＜0时，f′（x）＞g′（x）；
③如果y=f（x）是可导函数，则f′（x₀）=0是函数y=f（x）在x=x₀处取到极值的必要不充分条件；
④已知存在实数x使得不等式|x+1|-|x-1|≤a成立，则实数a的取值范围是a≥2．
其中正确的命题是

设函数f（x）=ax，g（x）=|x-a|，a∈R．
（1）当a=2时，解不等式f（x）＞g（x）；
（2）记F（x）=f（x）-g（x），判断F（x）的奇偶性，并说明理由；
（3）设G（x）=f（x）g（x），且G（x）在[1，+∞）上递增，求实数a的取值范围．

定义：两个连续函数（图象不间断）f（x）、g（x）在区间[a，b]上都有意义，则称函数|f（x）+g（x）|在[a，b]上的最大值叫做函数f（x）与g（x）在区间[a，b]上的“绝对和”．已知函数f（x）=x³，g（x）=x³-3ax²+2．
（I）若函数y=g（x）在点P（1，g（1））处的切线与直线y=x+2平行，求a的值；
（II）在（I）的条件下求汉顺f（x）与g（x）在区间[0，2]上的“绝对值”
（Ⅲ）记f（x）与g（x）在区间[0，2]上的“绝对和”为 $数学公式$ ，且h（a）=2，试求a的取值范围．

定义：两个连续函数（图象不间断）f（x）、g（x）在区间[a，b]上都有意义，则称函数|f（x）+g（x）|在[a，b]上的最大值叫做函数f（x）与g（x）在区间[a，b]上的“绝对和”．已知函数f（x）=x³，g（x）=x³-3ax²+2．
（I）若函数y=g（x）在点P（1，g（1））处的切线与直线y=x+2平行，求a的值；
（II）在（I）的条件下求汉顺f（x）与g（x）在区间[0，2]上的“绝对值”
（Ⅲ）记f（x）与g（x）在区间[0，2]上的“绝对和”为

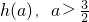，且h（a）=2，试求a的取值范围．