题目内容
(2012•盐城一模)已知函数f(x)=
sinxcosx-cos2x+
(x∈R).
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[0,
]上的函数值的取值范围.
| 3 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[0,
| π |
| 4 |
分析:(1)先降幂扩角,再利用辅助角公式化简,进而可求函数f(x)的最小正周期;
(2)根据x∈[0,
],可确定2x-
∈[-
,
],从而可求函数f(x)在区间[0,
]上的函数值的取值范围.
(2)根据x∈[0,
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
解答:解:(1)因为f(x)=
sin2x-
cos2x…(4分)
=sin(2x-
)…(6分)
故f(x)的最小正周期为π…(8分)
(2)当x∈[0,
]时,2x-
∈[-
,
]…(10分)
∴sin(2x-
)∈[-
,
]
故所求的值域为[-
,
]…(14分)
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
故f(x)的最小正周期为π…(8分)
(2)当x∈[0,
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴sin(2x-
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
故所求的值域为[-
| 1 |
| 2 |
| ||
| 2 |
点评:本题重点考查三角恒等变换,考查三角函数的性质,解题的关键是将函数式进行化简,利用三角函数的性质进行求解.

练习册系列答案
相关题目
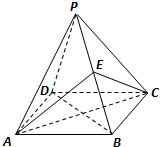 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.