题目内容
(2012•盐城一模)已知x、y、z均为正数,求证:
(
+
+
)≤
.
| ||
| 3 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
|
分析:已知x、y、z均为正数,根据柯西不等式(a12+a22+a32)(b12+b22+b32)≥(a1b1+a2b2+a3b3)2,可得(12+12+12)(
+
+
)≥(
+
+
)2然后进行化简,从而进行证明.
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| z2 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
解答:证明:由柯西不等式得(12+12+12)(
+
+
)≥(
+
+
)2…(5分)
则
×
≥
+
+
,
即
(
+
+
)≤
…(10分)
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| z2 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
则
| 3 |
|
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
即
| ||
| 3 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
|
点评:此题主要是柯西不等式的应用,只是进行简单的变形而已,此题比较简单.

练习册系列答案
相关题目
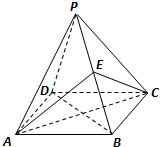 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.