题目内容
在正方体 中,
中, 为正方形
为正方形 中心,则
中心,则 与平面
与平面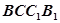 所成角的正切值为 ( )
所成角的正切值为 ( )
 中,
中, 为正方形
为正方形 中心,则
中心,则 与平面
与平面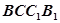 所成角的正切值为 ( )
所成角的正切值为 ( )A. | B. | C. | D. |
D
 |
取AD中点E,连OE,
 则
则 ,
, 是
是 与平面
与平面 所成的角;
所成的角;
 就等于
就等于 与平面
与平面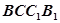 所成的角;设正方体棱长为2,则
所成的角;设正方体棱长为2,则 所以
所以 故选D
故选D
练习册系列答案
相关题目
题目内容
 中,
中, 为正方形
为正方形 中心,则
中心,则 与平面
与平面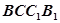 所成角的正切值为 ( )
所成角的正切值为 ( )A. | B. | C. | D. |
 |
 则
则 ,
, 是
是 与平面
与平面 所成的角;
所成的角;
 就等于
就等于 与平面
与平面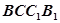 所成的角;设正方体棱长为2,则
所成的角;设正方体棱长为2,则 所以
所以 故选D
故选D