Question

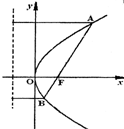
如图，已知AB是过抛物线y²=2px（p＞0）的焦点的弦，F为抛物线的焦点，点A（x₁，y₁），B（x₂，y₂）．
求证：
（1）|AB|=x₁+x₂+p；
（2）y₁y₂=-p²，x₁x₂=

p2

4

；
（3）（理科）直线的倾斜角为θ时，求弦长|AB|．
（3）（文科）当p=2，直线AB的倾斜角为

π

4

时，求弦长|AB|．

Answer 1

（1）证明：∵AB是过抛物线y²=2px（p＞0）的焦点的弦，
∴由抛物线定义可得|AB|=x₁+

p

2

+x₂+

p

2

=x₁+x₂+p；
（2）证明：设直线AB的方程为x=my+

p

2

，代入y²=2px，可得y²-2pmy-p²=0
∴y₁y₂=-p²，∴x₁x₂=

p2

4

；
（3）（理科）由（2）知，y₁y₂=-p²，y₁+y₂=2pm，∴

y

21

+

y

22

=（y₁+y₂）²-2y₁y₂=4p²m²+2p²，
∴

y

21

+

y

22

=2p（x₁+x₂）=4p²m²+2p²，∴x₁+x₂=2pm²+p，
∴θ=90°时，m=0，∴|AB|=2p；θ≠90°时，m=

1

tanθ

，|AB|=

2p

tan2θ

+2p；
（4）（文科）由（3）（理科）知，|AB|=

2p

tan2θ

+2p=8．