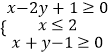题目内容
【题目】如图，设Ox、Oy是平面内相交成45°角的两条数轴， 
、 
分别是x轴、y轴正方向同向的单位向量，若向量 
=x +y ，则把有序数对（x，y）叫做向量 在坐标系xOy中的坐标，在此坐标系下，假设 
=（﹣2，2 
）， 
=（2，0）， 
=（5，﹣3 ），则下列命题不正确的是（ ）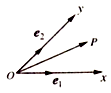 
A. =（1，0）
B.| |=2 
C. ∥ 
D. ⊥
【答案】B
【解析】解： 
=1× +0× ，∴ =（1，0）；故A正确； 由余弦定理可知| 
|= 
=2，故B错误；
∵ 
= 
=（3，﹣3 
）=﹣ 
，∴ ∥ ，故C正确； 的直角坐标为（0，2）， 
的直角坐标系为（2，0），
∴ 
．故D正确．
故选B．
利用定义判断A，根据余弦定理判断B，根据向量共线定理判定C，转化为正交分解判断D．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
