题目内容
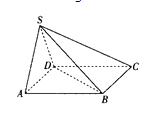
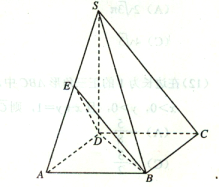
【题目】在三棱柱![]() 中,底面
中,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,侧面
为斜边的等腰直角三角形,侧面![]() 是菱形且与底面
是菱形且与底面![]() 垂直,
垂直,![]() ,点
,点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 上靠近
上靠近![]() 点的三等分点.
点的三等分点.
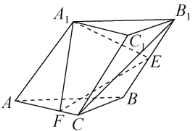
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 交于
交于![]() ,连接
,连接![]() ,通过证明
,通过证明![]() //
//![]() ,即可得证线面平行;
,即可得证线面平行;
(2)以![]() 中点
中点![]() ,建立空间直角坐标系,求得两个平面的法向量,通过向量法即可求得二面角的余弦值.
,建立空间直角坐标系,求得两个平面的法向量,通过向量法即可求得二面角的余弦值.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
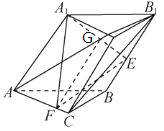
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 于
于![]() ,
,
因为![]() ,所以
,所以![]() 是线段
是线段![]() 的中点.
的中点.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,连接
,连接![]() ,
,
因为![]() 是等边三角形,
是等边三角形,![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() .
.
所以![]() 平面
平面![]() .
.
如图,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线
所在直线
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标,
轴建立空间直角坐标,

不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
则![]() 的中点
的中点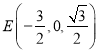 ,
,
从而![]()
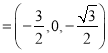 ,
,![]()
![]() .
.
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,
则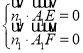 ,即
,即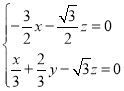 ,
,
不妨取![]() ,得
,得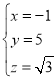 ,即
,即![]()
![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,
,
则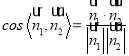
![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
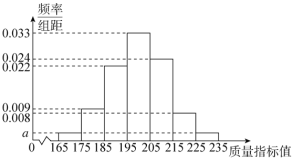
【题目】大荔县某高中一社团为调查学生学习围棋的情况,随机抽取了![]() 名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于
名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于![]() 分钟的学生称为“围棋迷”.
分钟的学生称为“围棋迷”.
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |

(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)现在从参与本次抽样调查的![]() 名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取
名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取![]() 名学生参与围棋知识竞赛,再从
名学生参与围棋知识竞赛,再从![]() 人中任选
人中任选![]() 人参与知识竞赛的赛前保障工作.求选到的
人参与知识竞赛的赛前保障工作.求选到的![]() 人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
附:![]() ,
,
|
|
|
|
|
|