题目内容
13．
已知函数f（x）=x2-4|x|+3，x∈R．（1）判断函数的奇偶性并将函数写成分段函数的形式；
（2）画出函数的图象，根据图象写出它的单调区间；
（3）若函数f（x）的图象与y=a的图象有四个不同交点，则实数a的取值范围．
分析 （1）由f（-x）=f（x）得函数为偶函数，对x分类讨论：x≥0，x＜0得分段函数的解析式；
（2）由分段函数分两种情况作二次函数的图象；
（3）由图象可知函数的单调区间及值域．
解答 解：（1）因为函数的定义域为R，关于坐标原点对称，
且f（-x）=（-x）2-4|-x|+3=x2-4|x|+3=f（x），
故函数为偶函数．
f（x）=x2-4|x|+3=$\left\{\begin{array}{l}{{x}^{2}-4x+3，x≥0}\\{{x}^{2}+4x+3，x＜0}\end{array}\right.$
（2）如图，
单调增区间为：：[-2，0），[2，+∞），
单调减区间为（-∞，-2），[0，2]．
（3）由函数的图象可知：函数f（x）的图象与y=a的图象有四个不同交点，则实数a的取值范围：（-1，3）．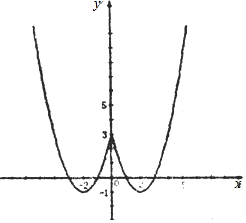
点评 本题考查函数的图象及性质．考查数形结合思想，转化思想以及计算能力．
练习册系列答案
相关题目
3．方程x5-x-1=0的一个正零点的存在区间可能是（ ）
| A． | [0，1] | B． | [1，2] | C． | [2，3] | D． | [3，4] |
4．
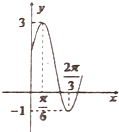如图所示，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分，则函数解析式是（ ）
如图所示，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分，则函数解析式是（ ）| A． | $y=2sin（2x+\frac{π}{6}）+1$ | B． | $y=sin（2x+\frac{π}{3}）+1$ | C． | $y=2sin（\frac{1}{2}x+\frac{π}{6}）+2$ | D． | $y=sin（2x+\frac{π}{3}）+2$ |