题目内容
【题目】已知函数![]() ,其中
,其中![]() 且
且![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)证明:当![]() 时,函数
时,函数![]() 在
在![]() 上为减函数;
上为减函数;
(3)求函数![]() 的值域.
的值域.
【答案】(1)![]() 为偶函数;(2)证明见解析;
为偶函数;(2)证明见解析;
(3)当![]() 时,值域为
时,值域为![]() ;当
;当![]() 时,值域为
时,值域为![]() .
.
【解析】试题分析:(1)先判断定义域是否关于原点对称,再验证![]() 还是
还是![]() ;(2)按照单调性的定义进行证明即可;(3)令
;(2)按照单调性的定义进行证明即可;(3)令![]() ,由条件可得
,由条件可得![]() ,
,
然后分![]() 和
和![]() 两种情况求函数的值域。
两种情况求函数的值域。
试题解析:
(1)要使函数有意义,需满足![]() ,
,
解得![]()
∴ 函数![]() 的定义域为
的定义域为![]() ,
,
∵![]()
∴函数![]() 为偶函数。
为偶函数。
(2)由题意得![]() ,
,
设![]() ,且
,且![]() ,则
,则
![]()
∵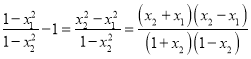
又 ![]() ,
, ![]() ,
, ![]()
∴![]() ,
,
∴![]()
又![]()
∴![]()
∴![]()
∴ 函数![]() 在
在![]() 上为减函数.
上为减函数.
(3)令![]() ,则
,则![]() 。
。
∵![]() ,
,
∴![]()
当![]() 时,
时, ![]() ,故函数
,故函数![]() 的值域为
的值域为![]() ,
,
当![]() 时,
时, ![]() ,故函数
,故函数![]() 的值域为
的值域为![]() 。
。
综上可得当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ;当
;当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() 。
。

练习册系列答案
相关题目
【题目】某商场经营一批进价为![]() 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
销售价( |
|
|
|
|
日销售量( |
|
|
|
|
日销售额( |
| |||
日销售利润( |
|
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对![]() 的对应点,并写出
的对应点,并写出![]() 与
与![]() 的一个函数关系式;
的一个函数关系式;
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求![]() 与
与![]() 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?