题目内容

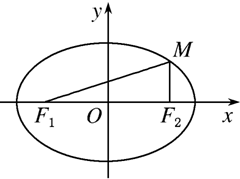精英家教网如图所示，F1，F2分别为椭圆的左、右焦点，椭圆上点M的横坐标等于右焦点的横坐标，其纵坐标等于短半轴长的
23
，求椭圆的离心率．
分析：设椭圆的长半轴、短半轴、半焦距长分别为a、b、c，可得M（c，
2
3
b），利用勾股定理与椭圆的定义建立关于a、b、c的等式，化简整理得b=
2
3
a，从而得出c=
a2-b2
=
5
3
a，即可算出该椭圆的离心率．
解答：解：设椭圆的长半轴、短半轴、半焦距长分别为a、b、c，
可得焦点为F1（-c，0）、F2（c，0），点M的坐标为（c，
2
3
b），
∵Rt△MF1F2中，F1F2⊥MF2，
∴|F1F2|2+|MF2|2=|MF1|2，即4c2+
4
9
b2=|MF1|2，
根据椭圆的定义得|MF1|+|MF2|=2a，
可得|MF1|2=（2a-|MF2|）2=（2a-
2
3
b）2，
∴（2a-
2
3
b）2=4c2+
4
9
b2，整理得4c2=4a2-
8
3
ab，
可得3（a2-c2）=2ab，所以3b2=2ab，解得b=
2
3
a，
∴c=
a2-b2
=
5
3
a，
因此可得e=
c
a
=
5
3
，
即该椭圆的离心率等于
5
3
．
点评：本题已知椭圆满足的条件，求椭圆的离心率的大小．着重考查了椭圆的定义、标准方程与简单几何性质等知识，考查了勾股定理的应用，属于中档题．
练习册系列答案
相关题目
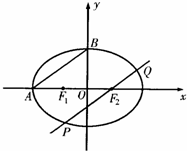精英家教网如图所示，F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右两个焦点，A，B为两个顶点，已知椭圆C上的点到F1，F2两点的距离之和为4且b=
3
．
（1）求椭圆C的方程和焦点坐标；
（2）过椭圆C的焦点F2作AB的平行线交椭圆于P，Q两点，求△F1PQ的面积．
精英家教网如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1 (a＞b＞0)的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点(1，
3
2
)到F1、F2两点的距离之和为4．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，
3
2
）到F1、F2两点的距离之和为4．
（1）求椭圆C的方程和焦点坐标；
（2）设点M是椭圆上的动点N（0，
1
2
），求|MN|的最大值．
（3）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1 (a＞b＞0)的左、右两个焦点，A、B为两个顶点；已知顶点B(0，
3
)到F1、F2两点的距离之和为4．
（1）求椭圆C的方程；
（2）证明：椭圆C上任意一点M（x0，y0）到右焦点F2的距离的最小值为1．
（3）作AB的平行线交椭圆C于P、Q两点，求弦长|PQ|的最大值，并求|PQ|取最大值时△F1PQ的面积．
（2013•牡丹江一模）如图所示，F1和F2分别是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点，A和B是以O为圆心，|OF1|为半径的圆与该双曲线左支的两个交点，且△F2AB是等边三角形，则离心率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网