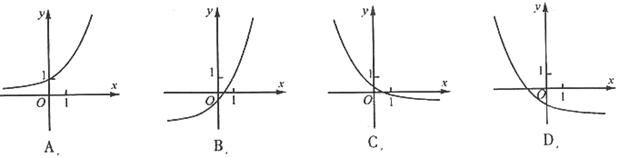
题目内容
函数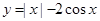 的图象大致是
的图象大致是 
C
解析试题分析:根据已知的解析式可知函数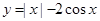 ,是有偶函数
,是有偶函数 两个偶函数相加得到的,那么利用奇偶性的性质可知为偶函数,排除选项D,B,同时利用函数在x取得正数时,那么
两个偶函数相加得到的,那么利用奇偶性的性质可知为偶函数,排除选项D,B,同时利用函数在x取得正数时,那么
的点有无穷多个,那么说明极值点不是有限个,排除A,只有选C.
考点:本试题考查了函数的图像的的表示。
点评:对于给定的解析式,求解函数的图像问题,一般从函数的性质或者特殊点入手,采用排除法来求解函数的图像,也是高考中常考查的知识点,比较重要,注意解题方法,属于中档题。

练习册系列答案
相关题目
下列两个函数为相等函数的是( )
A. 与 与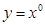 |
B.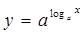 与 与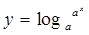 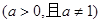 |
C.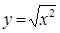 与 与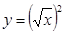 |
D.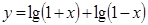 与 与 |
已知-2<x<0,则 的最小值为( )
的最小值为( )
| A.2 | B.3 | C. | D.-2 |
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
已知函数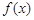 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
 的值属于区间
的值属于区间
A. | B. | C. | D. |
设函数 的定义域为
的定义域为 ,
,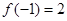 ,对于任意的
,对于任意的 ,
, ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
下列四个函数:(1) (2)
(2) (3)
(3)
(4) ,其中同时满足:①
,其中同时满足:① ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量 ,都有
,都有 的函数个数为
的函数个数为
| A.1 | B.2 | C.3 | D.4 |
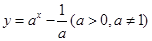 的图象可能是 ( )
的图象可能是 ( )