题目内容
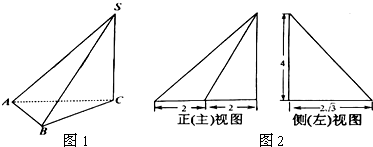
15.点P在直径为5的球面上,过P作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )| A. | 2$\sqrt{14}$ | B. | 2$\sqrt{70}$ | C. | $\sqrt{70}$ | D. | $\sqrt{14}$ |
分析 设三条弦长分别是a,2a,h,则a2+(2a)2+h2=25,三条弦长之和S=3a+h,进而可得14a2-6aS+S2-25=0,由△≥0得三条弦长之和的最大值.
解答 解:设三条弦长分别是a,2a,h,则a2+(2a)2+h2=25,即5a2+h2=25,三条弦长之和S=3a+h,
将h=S-3a代入5a2+h2=25,得14a2-6aS+S2-25=0,由△≥0得S2≤70.
故选:C.
点评 本题考查圆的内接多面体,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目