题目内容
函数f(x)=sin(ωx+ϕ)(ω>0,0≤ϕ≤π)是R上的偶函数,(1)求ϕ的值.
(2)若f(x)图象上的点关于M(
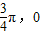 )对称,①求ω满足的关系式;②若f(x)在区间[0,
)对称,①求ω满足的关系式;②若f(x)在区间[0,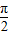 ]上是单调函数,求ω的值.
]上是单调函数,求ω的值.
【答案】分析:(1)根据正弦函数的图象与性质,结合题意得sinϕ=±1,结合题设0≤ϕ≤π,解之可得ϕ=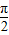 ;
;
(2)由(1)可得f(x)=cosωx,由余弦曲线的对称中心的公式,建立关于ω的等式,算出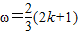 ,其中k=0,1,2,….结合f(x)在区间[0,
,其中k=0,1,2,….结合f(x)在区间[0,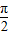 ]上的单调性,即可解出
]上的单调性,即可解出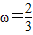 或ω=2.
或ω=2.
解答:解:(1)由f(x)是偶函数,可得f(0)=±1,
故sinϕ=±1,即ϕ=kπ+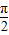 ,
,
结合题设0≤ϕ≤π,解之得ϕ=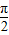 ,…(5分)
,…(5分)
(2)由(1)知f(x)=sin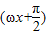 =cosωx,
=cosωx,
∵f(x)图象上的点关于M(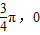 )对称,
)对称,
∴f(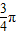 )=cos
)=cos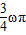 =0,故
=0,故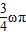 =
=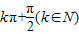
即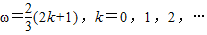 .…(10分)
.…(10分)
∵f(x)在区间[0,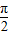 ]上是单调函数,可得
]上是单调函数,可得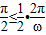 ,即ω≤2
,即ω≤2
又∵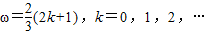 .
.
∴综合以上条件,可得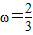 或ω=2.…(16分)
或ω=2.…(16分)
点评:本题给出函数f(x)=sin(ωx+ϕ)满足的条件,求参数的值,着重考查了三角函数的图象与性质、函数的奇偶性和图象的对称性等知识,属于中档题.
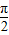 ;
;(2)由(1)可得f(x)=cosωx,由余弦曲线的对称中心的公式,建立关于ω的等式,算出
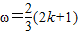 ,其中k=0,1,2,….结合f(x)在区间[0,
,其中k=0,1,2,….结合f(x)在区间[0,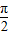 ]上的单调性,即可解出
]上的单调性,即可解出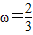 或ω=2.
或ω=2.解答:解:(1)由f(x)是偶函数,可得f(0)=±1,
故sinϕ=±1,即ϕ=kπ+
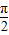 ,
,结合题设0≤ϕ≤π,解之得ϕ=
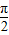 ,…(5分)
,…(5分)(2)由(1)知f(x)=sin
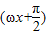 =cosωx,
=cosωx,∵f(x)图象上的点关于M(
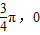 )对称,
)对称,∴f(
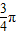 )=cos
)=cos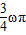 =0,故
=0,故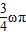 =
=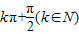
即
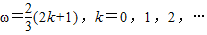 .…(10分)
.…(10分)∵f(x)在区间[0,
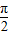 ]上是单调函数,可得
]上是单调函数,可得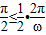 ,即ω≤2
,即ω≤2又∵
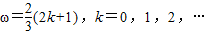 .
.∴综合以上条件,可得
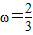 或ω=2.…(16分)
或ω=2.…(16分)点评:本题给出函数f(x)=sin(ωx+ϕ)满足的条件,求参数的值,着重考查了三角函数的图象与性质、函数的奇偶性和图象的对称性等知识,属于中档题.

练习册系列答案
相关题目
 函数f(x)=sin(ωx+?)(x∈R,ω>0,0≤?<2π)的部分图象如图,则
函数f(x)=sin(ωx+?)(x∈R,ω>0,0≤?<2π)的部分图象如图,则