题目内容
4.在平面直角坐标系xOy中,P为双曲线x2-y2=1右支上的一个动点.若点P到直线x-y+1=0 的距离大于m恒成立,则实数 m的最大值为$\frac{\sqrt{2}}{2}$.分析 双曲线x2-y2=1的渐近线方程为x±y=0,c的最大值为直线x-y+1=0与直线x-y=0的距离.
解答 解:由题意,双曲线x2-y2=1的渐近线方程为x±y=0,
由点P到直线x-y+1=0的距离大于m恒成立,
∴m的最大值为直线x-y+1=0与渐近线x-y=0的距离,即d=$\frac{丨1丨}{\sqrt{{1}^{2}+{1}^{2}}}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查双曲线的性质,考查两平行线之间的距离公式,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
14.已知正项数列{an}的前n项和为Sn,当n≥2时,(an-Sn-1)2=SnSn-1,且a1=1,设b${\;}_{n}=lo{g}_{2}\frac{{a}_{n+1}}{6}$,则b1+b2+…+b10等于( )
| A. | 64 | B. | 72 | C. | 80 | D. | 90 |
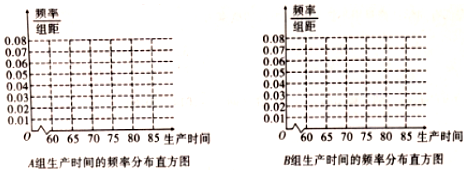
12.为了了解培训讲座对某工厂工人生产时间(生产一个零件所用的时间,单位:分钟)的影响.从工厂随机选取了200名工人,再将这200名工人随机的分成A,B两组,每组100人.A组参加培训讲座,B组不参加.培训讲座结束后A,B两组中各工人的生产时间的调查结果分别为表1和表2.
表1:
表2
(1)甲、乙两名工人是随机抽取到的200名工人中的两人,求甲、乙分在不同组的概率;
(2)完成图3的频率分布直方图,比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小;(不用计算,可通过直方图直接回答结论)
(3)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关?
下面临界值表仅供参考:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
表1:
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) |
| 人数 | 30 | 40 | 20 | 10 |
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) |
| 人数 | 10 | 25 | 20 | 30 | 15 |
(2)完成图3的频率分布直方图,比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小;(不用计算,可通过直方图直接回答结论)

(3)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关?
| 生产时间小于70分钟 | 生产时间不小于70分钟 | 合计 | |
| A组工人 | a= | b= | |
| B组工人 | c= | d= | |
| 合计 | n= |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.小张以10元一股的价格购买了一支股票,他将股票当天的最高价格y(元)与第t个交易日(其中0≤t≤24)进行了记录,得到有关数据如表(不考虑股票交易涨跌停规律):
他经过研究后认为单支股票当天的最高价格y(元)是第t个交易日的函数y=f(t),并且认为y=f(t)的曲线可近似地看作函数f(t)=Asinωt+b的图象,请根据小张的观点解决下列问题.
(1)试根据以上数据,求出函数f(t)=Asinωt+b的振幅、最小正周期和表达式;
(2)小张认为当股票价格不低于11.5元时抛售股票比较合理,请问在股票最高价格波动的一个周期内小张有几天可以抛售股票?
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/元 | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 |
(1)试根据以上数据,求出函数f(t)=Asinωt+b的振幅、最小正周期和表达式;
(2)小张认为当股票价格不低于11.5元时抛售股票比较合理,请问在股票最高价格波动的一个周期内小张有几天可以抛售股票?
10.函数f(x)=x2-(2a-1)x-3在$({\frac{3}{2},+∞})$上是增函数,则实数a的范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≤2 | D. | a≥2 |
 如图,在△ABC中,内角A、B、C所对的边分别是a、b、c,$B=\frac{π}{3}$,a=2.
如图,在△ABC中,内角A、B、C所对的边分别是a、b、c,$B=\frac{π}{3}$,a=2.