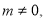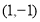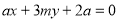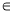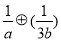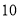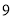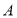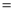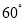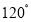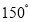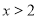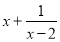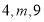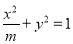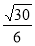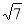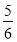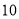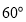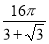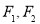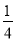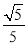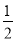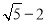题目内容
已知椭圆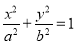 (
(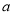 >
>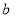 >0)的离心率
>0)的离心率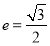 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线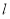 与椭圆相交于不同的两点
与椭圆相交于不同的两点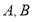 ,已知点
,已知点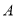 的坐标为(
的坐标为( 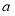 ,0),点
,0),点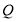 (0,
(0,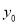 )在线段
)在线段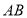 的垂直平分线上,且
的垂直平分线上,且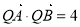 ,求
,求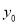 的值.
的值.
(1)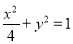 (2)
(2)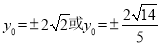
【解析】
试题分析:(1)连接椭圆的四个顶点得到的菱形的面积为4即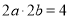 ,在结合
,在结合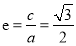 和
和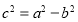 可解得
可解得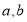 的值。(2)分析可知直线
的值。(2)分析可知直线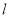 斜率存在,可设其方程为
斜率存在,可设其方程为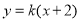 ,将直线方程和椭圆方程联立消去
,将直线方程和椭圆方程联立消去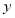 整理为关于
整理为关于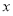 的一元二次方程,由韦达定理可得根与系数的关系,其中一个根为
的一元二次方程,由韦达定理可得根与系数的关系,其中一个根为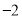 另一个跟为点
另一个跟为点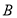 的横坐标。根据
的横坐标。根据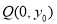 在线段
在线段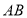 的垂直平分线上和
的垂直平分线上和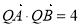 可求
可求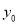 的值。需注意对
的值。需注意对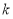 为0时的讨论。
为0时的讨论。
试题解析:(1)【解析】
由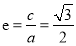 , 1分
, 1分
得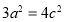 ,再由
,再由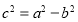 ,得
,得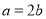 2分
2分
由题意可知,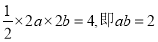 3分
3分
解方程组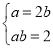 得:
得: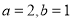
所以椭圆的方程为: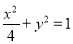 4分
4分
(2)【解析】
由(1)可知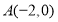 .设
.设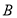 点的坐标为
点的坐标为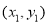 ,
,
直线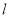 的斜率显然所在,设为
的斜率显然所在,设为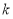 ,则直线
,则直线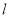 的方程为
的方程为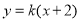 , 5分
, 5分
于是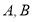 两点的坐标满足方程组
两点的坐标满足方程组 ,由方程组消去
,由方程组消去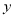 并整理,
并整理,
得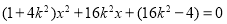 6分
6分
由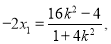 得
得 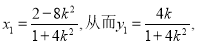 8分
8分
设线段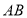 是中点为
是中点为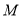 ,则
,则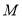 的坐标为
的坐标为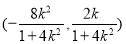
以下分两种情况:
①当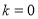 时,点
时,点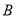 的坐标为
的坐标为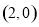 .线段
.线段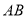 的垂直平分线为
的垂直平分线为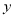 轴,于是
轴,于是
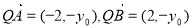
由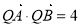 得
得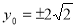 10分
10分
②当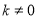 时,线段
时,线段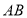 的垂直平分线方程为
的垂直平分线方程为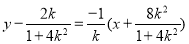
令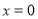 ,解得
,解得
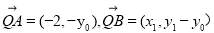
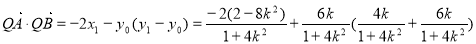
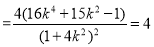
整理得 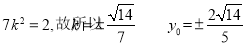 13分
13分
综上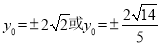 . 14分
. 14分
考点:1椭圆的标准方程;2直线和椭圆的位置关系。

练习册系列答案
相关题目