Question

如图，已知四边形ABCD是边长为4的正方形，E、F分别为AD、AB的中点，GC垂直于ABCD所在的平面，且GC=2，求点B到平面FEG的距离.

Answer 1

分析：用点到平面的距离公式求点B到平面FEG的距离.

解：解法一：以、,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系，则G（0,0,2),B(0,4,0),A(4,4,0),D(4,0,0),E(4,2,0),F(2,4,0).

故=（4，2，-2），=（2，4，-2）.

设n₀=(x,y,z)是平面EFG的单位法向量,则有

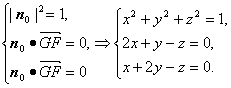
取z＞0，得x=y=,z=.

所以n₀=(1,1,3).

又因为=（0，4，-2），

所以d=|n₀·|=|(1,1,3)·(0,4,-2)|=,

即点B到平面FEG的距离为.

解法二:等体积转化,根据V_B—FEG=V_G—BEF,

因为四边形ABCD为正方形,E,F分别为DA,AB的中点,所以CE=CF=2.

所以GE=GF=2,EF=2.

所以S_△GEF=.

所以(2)·h=(×2×2)×2.

所以h==.

点拨：求点到平面的距离有三种方法：（1）常规方法：作、证、求，即作出该距离，证明它是点到平面的距离，再求出；（2）等体积转化法，即构造出一个封闭的几何体，使所求的距离为一个底面上的高；（3）向量法：设n是平面α的法向量，AB是平面α的一条斜线，A∈α,则点B到平面α的距离d为|AB·n₀|(其中n₀=).