题目内容
在平面直角坐标系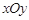 中,以坐标原点
中,以坐标原点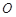 为极点,
为极点,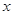 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线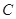 的极坐标方程为
的极坐标方程为 ,直线
,直线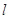 的参数方程为
的参数方程为 为参数,
为参数,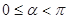 ).
).
(1)化曲线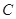 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2)若直线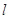 经过点
经过点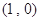 ,求直线
,求直线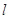 被曲线
被曲线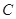 截得的线段
截得的线段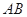 的长.
的长.
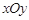 中,以坐标原点
中,以坐标原点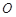 为极点,
为极点,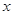 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线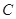 的极坐标方程为
的极坐标方程为 ,直线
,直线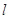 的参数方程为
的参数方程为 为参数,
为参数,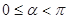 ).
).(1)化曲线
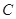 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;(2)若直线
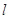 经过点
经过点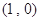 ,求直线
,求直线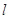 被曲线
被曲线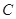 截得的线段
截得的线段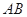 的长.
的长.(1) 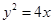 ;(2)8
;(2)8
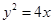 ;(2)8
;(2)8试题分析:(1)极坐标化为直角坐标的基本公式是
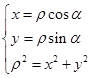 ,本小题要在极坐标方程的两边乘以一个
,本小题要在极坐标方程的两边乘以一个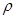 .再根据基本转化公式,即可化简.
.再根据基本转化公式,即可化简.(2)解(一)将直线的参数方程化为直角方程,在联立抛物线方程,消去y即可得到一个关于x的一元二次方程,从而利用韦达定理,以及弦长公式求出弦长.解(二)由直线的参数方程与抛物线方程联立.再根据弦长公式,利用韦达定理即可求出弦长.
试题解析:解法(一):(1)由
 得
得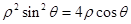 ,即曲线C的直角坐标方程为
,即曲线C的直角坐标方程为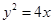 .
.(2)由直线
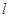 经过点(1,0),得直线
经过点(1,0),得直线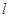 的直角坐标系方程是
的直角坐标系方程是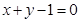 ,联立
,联立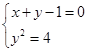 ,消去y,得
,消去y,得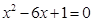 ,又点(1,0)是抛物线的焦点,由抛物线定义,得弦长
,又点(1,0)是抛物线的焦点,由抛物线定义,得弦长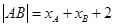 =6+2=8.
=6+2=8.解法(二):(1)同解法一.
(2)由直线
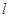 经过点(1,0),得
经过点(1,0),得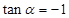 ,直线
,直线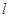 的参数方程为
的参数方程为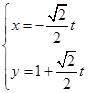 将直线
将直线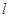 的参数方程代入
的参数方程代入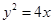 ,得
,得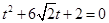 ,所以
,所以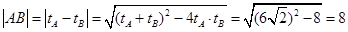 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
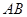 为抛物线
为抛物线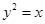 上的动弦,且
上的动弦,且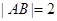 , 则弦
, 则弦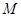 到
到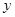 轴的最小距离为
轴的最小距离为 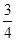
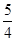
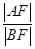 的值等于( ).
的值等于( ).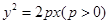 的焦点的距离是5,那么P= .
的焦点的距离是5,那么P= . 与抛物线
与抛物线 相交于
相交于 、
、 两点,
两点, 为抛物线
为抛物线 的焦点.若
的焦点.若 ,则实数
,则实数 .
.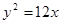 上与焦点的距离等于6的点横坐标是( )
上与焦点的距离等于6的点横坐标是( )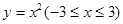 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 .