题目内容
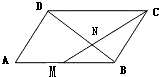如图所示，在平行四边形ABCD中，点M是AB的中点，点N是BD上一点，BN=| 1 | 3 |
分析：利用向量的运算法则将
，
两向量用基底
，
表示，得到
，
的关系，利用向量共线的充要条件得到两向量共线，进一步得出三点共线．
| MN |
| MC |
| AB |
| AD |
| MN |
| MC |
解答：解：设
=
，
=
∴
=
+
=
+
=
+
(
-
)=
+
(
-
)=
+
=
+
=
+
=
+
=3
∴
∥
又
，
有公共点M
∴M，N，C三点共线．
| AB |
| a |
| AD |
| b |
∴
| MN |
| MB |
| BN |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| BD |
| 1 |
| 2 |
| a |
| 1 |
| 3 |
| AD |
| AB |
| 1 |
| 2 |
| a |
| 1 |
| 3 |
| b |
| a |
| 1 |
| 6 |
| a |
| 1 |
| 3 |
| b |
| MC |
| MB |
| BC |
| 1 |
| 2 |
| AB |
| AD |
| 1 |
| 2 |
| a |
| b |
| MN |
∴
| MN |
| MC |
又
| MN |
| MC |
∴M，N，C三点共线．
点评：本题考查向量的运算法则、向量共线的充要条件、利用向量共线解决三点共线．
练习册系列答案
灵星计算小达人系列答案
相关题目
，那么在图②中所示的平行六面体
中，
等于（ ）
