题目内容
已知函数f(x)=x3-3x2+2(0<x<2)的反函数为f-1(x),则
- A.
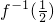 <
<
- B.
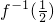 >
>
- C.
 <
<
- D.
 >
>
B
分析:根据题意通过判断原函数的单调性来判断反函数的单调性,即可得到反函数在区间[-2,2]上是单调减函数,进而得到答案.
解答:由题意可得:函数f(x)=x3-3x2+2(0<x<2),
所以f′(x)=3x2-6x=3x(x-2),
所以f′(x)=3x2-6x=3x(x-2)<0在(0,2)上恒成立,
所以f(x)在(0,2)上是单调减函数,即x越大y就越小,并且y∈[-2,2].
又因为函数f(x)=x3-3x2+2(0<x<2)的反函数为f-1(x),
所以f-1(x)再[-2,2]上是单调减函数,
所以 .
.
故选B.
点评:解决此类问题的关键是熟练掌握导数与函数单调性的关系,以及掌握原函数与反函数的单调性具有一致性,并且结合正确的运算.
分析:根据题意通过判断原函数的单调性来判断反函数的单调性,即可得到反函数在区间[-2,2]上是单调减函数,进而得到答案.
解答:由题意可得:函数f(x)=x3-3x2+2(0<x<2),
所以f′(x)=3x2-6x=3x(x-2),
所以f′(x)=3x2-6x=3x(x-2)<0在(0,2)上恒成立,
所以f(x)在(0,2)上是单调减函数,即x越大y就越小,并且y∈[-2,2].
又因为函数f(x)=x3-3x2+2(0<x<2)的反函数为f-1(x),
所以f-1(x)再[-2,2]上是单调减函数,
所以
 .
.故选B.
点评:解决此类问题的关键是熟练掌握导数与函数单调性的关系,以及掌握原函数与反函数的单调性具有一致性,并且结合正确的运算.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|