题目内容
在函数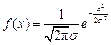 ,
,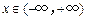 的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数
的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数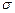 与曲线形状的关系,并运用指数函数的有关性质加以说明.
与曲线形状的关系,并运用指数函数的有关性质加以说明.
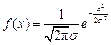 ,
,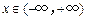 的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数
的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数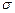 与曲线形状的关系,并运用指数函数的有关性质加以说明.
与曲线形状的关系,并运用指数函数的有关性质加以说明.曲线在x轴的上方;函数 为偶函数,其图象的对称轴为y轴;
为偶函数,其图象的对称轴为y轴; 时,
时, 有最大值
有最大值 ;
;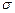 决定了曲线的“高矮”:
决定了曲线的“高矮”: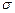 越大,曲线越“矮胖”,反之则越“瘦高”.
越大,曲线越“矮胖”,反之则越“瘦高”.
 为偶函数,其图象的对称轴为y轴;
为偶函数,其图象的对称轴为y轴; 时,
时, 有最大值
有最大值 ;
;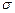 决定了曲线的“高矮”:
决定了曲线的“高矮”: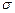 越大,曲线越“矮胖”,反之则越“瘦高”.
越大,曲线越“矮胖”,反之则越“瘦高”.由已知, ,且
,且 .
.
由指数函数的性质知 ,说明曲线在x轴的上方;又由
,说明曲线在x轴的上方;又由 知,函数
知,函数 为偶函数,其图象的对称轴为y轴;当
为偶函数,其图象的对称轴为y轴;当 趋向于无穷大时,
趋向于无穷大时, 趋向于0,即
趋向于0,即 趋向于0,说明其渐近线为
趋向于0,说明其渐近线为 轴;其中,
轴;其中, 时,(即在对称轴
时,(即在对称轴 的右侧),
的右侧), 随
随 的增大而减小,此时
的增大而减小,此时 单调递减;同理
单调递减;同理 在
在 时单调递增;由偶函数的对称性知,
时单调递增;由偶函数的对称性知, 时,
时, 有最大值
有最大值 ;
;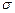 决定了曲线的“高矮”:
决定了曲线的“高矮”: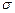 越大,曲线越“矮胖”,反之则越“瘦高”.
越大,曲线越“矮胖”,反之则越“瘦高”.
 ,且
,且 .
.由指数函数的性质知
 ,说明曲线在x轴的上方;又由
,说明曲线在x轴的上方;又由 知,函数
知,函数 为偶函数,其图象的对称轴为y轴;当
为偶函数,其图象的对称轴为y轴;当 趋向于无穷大时,
趋向于无穷大时, 趋向于0,即
趋向于0,即 趋向于0,说明其渐近线为
趋向于0,说明其渐近线为 轴;其中,
轴;其中, 时,(即在对称轴
时,(即在对称轴 的右侧),
的右侧), 随
随 的增大而减小,此时
的增大而减小,此时 单调递减;同理
单调递减;同理 在
在 时单调递增;由偶函数的对称性知,
时单调递增;由偶函数的对称性知, 时,
时, 有最大值
有最大值 ;
;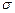 决定了曲线的“高矮”:
决定了曲线的“高矮”: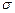 越大,曲线越“矮胖”,反之则越“瘦高”.
越大,曲线越“矮胖”,反之则越“瘦高”.
练习册系列答案
相关题目
 (
( )是一个随机变量,已知
)是一个随机变量,已知 ,又随机变量
,又随机变量 (
( )
) ,求
,求 ~
~ ,且
,且 ,则
,则 的方差为 .
的方差为 . ( )
( ) 



 服从正态分布
服从正态分布 ,若
,若 内取值的概率
内取值的概率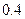 ,则
,则 内取值的概率为 .
内取值的概率为 .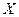 服从正态分布
服从正态分布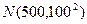 ,现有2500名考生,据往年录取率可推测今年约有1000名高考考生考上一类大学,估计今年一类大学的录取分数线为 分.(其中
,现有2500名考生,据往年录取率可推测今年约有1000名高考考生考上一类大学,估计今年一类大学的录取分数线为 分.(其中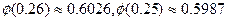 )
)