题目内容
 ⊙O半径为
⊙O半径为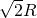 ,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.
,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.
(Ⅰ)当θ=90°时,求四面体D-ABC的表面积;
(Ⅱ)当θ=90°时,求异面直线AC与BD所成的角;
(Ⅲ)当θ为何值时,四面体D-ABC的体积 ?
?
 解:(I)由已知,易得AC=CB=BD=DA=2R,
解:(I)由已知,易得AC=CB=BD=DA=2R,∵DO⊥AB,CO⊥AB∴∠DOC为二面角的平面角θ,
在Rt△DOC中,得DC=2R
于是△ADC,△BCD是全等的正三角形,边长为2R,
而△ACB,△ADB为全等的等腰直角三角形.
∴四面体D-ABC的表面积=

=

=
 ;
;(II)(方法一)设AD中点为M,CD中点为N,
连MN,MO,则AC∥MN,BD∥MO,
则∠NMO为异面直线AC与BD所成的角,
连NO,由(1)可得MN=MO=NO=R,
所以∠NMO=60°.
(方法二)∵DO⊥AB,CO⊥AB,θ=90°
∴分别以OC,OB,OD为x轴、y轴、z轴建立空间直角坐标系,
则有
 ,
,
∴

设异面直线AC与BD所成的角所成的角为α,

则

所以异面直线AC与BD所成的角为60°;
(III)如图,作DG⊥CO于G,
∵AB⊥DO,AB⊥CO,∴AB⊥平面COD,从而AB⊥DG
∴DG⊥平面ABC,∴DG为四面体D-ABC的高,
在Rt△DOG中,
 ,
,∴
 ,
,当
 时,解得
时,解得 ,所以θ=30°或150°.
,所以θ=30°或150°.分析:(Ⅰ)当θ=90°时,先求底面面积再求侧面的高,然后求四面体D-ABC的表面积;
(Ⅱ)当θ=90°时,求异面直线AC与BD所成的角;
法一作出异面直线所成的角,然后求解即可.
法二建立空间直角坐标系,利用向量的数量积求解即可.
(Ⅲ)当θ为何值时,四面体D-ABC的体积
 ,先由此体积求出D到底面的距离,然后再求二面角的大小.
,先由此体积求出D到底面的距离,然后再求二面角的大小.点评:本题考查异面直线所成的角,棱锥的体积,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
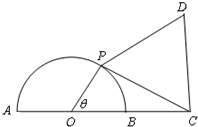 如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.
如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧. (2011•西城区二模)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为
(2011•西城区二模)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为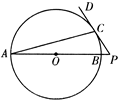 (1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=
(1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=