题目内容
已知数列 的前
的前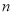 项和为
项和为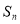 ,且
,且 ,
,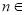 N*
N*
(1)求数列 的通项公式;
的通项公式;
(2)已知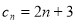 (
(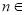 N*),记
N*),记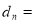
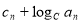 (
(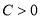 且
且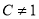 ),是否存在这样的常数
),是否存在这样的常数 ,使得数列
,使得数列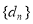 是常数列,若存在,求出
是常数列,若存在,求出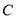 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列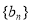 ,对于任意的正整数
,对于任意的正整数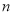 ,均有
,均有 成立,求证:数列
成立,求证:数列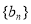 是等差数列;
是等差数列;
(1) 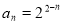 (
(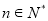 );(2)
);(2) 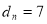 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)由题意可知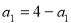 ,所以
,所以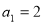 ,由
,由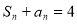 得
得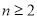 时,
时,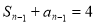 ,两式相减得,
,两式相减得, 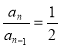 ,数列
,数列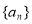 是以2为首项,公比为
是以2为首项,公比为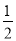 的等比数列,即可求出结果;(2)由于数列
的等比数列,即可求出结果;(2)由于数列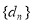 是常数列,所以
是常数列,所以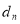 =
=
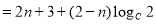
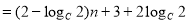 为常数,
为常数,
故,只有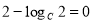 ,解得
,解得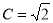 ,即可求出结果;(3)
,即可求出结果;(3)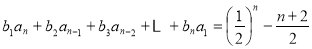 ,
, 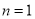 ,
, ,其中
,其中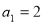 ,所以
,所以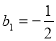 当
当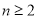 时,
时,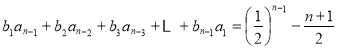 采用错位相减即可求出结果.
采用错位相减即可求出结果.
试题解析:【解析】
(1)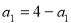 ,所以
,所以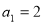 1分
1分
由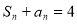 得
得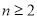 时,
时,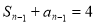 2分
2分
两式相减得,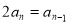 ,
,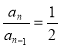 ,3分
,3分
数列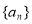 是以2为首项,公比为
是以2为首项,公比为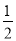 的等比数列,所以
的等比数列,所以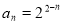 (
(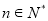 )5分
)5分
(2)由于数列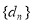 是常数列
是常数列
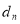 =
=
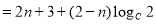 6分
6分
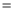
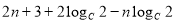
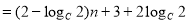 为常数7分
为常数7分
只有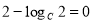 ,8分;解得
,8分;解得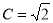 ,9分
,9分
此时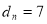 10分
10分
(3)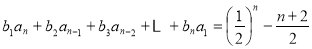 ①
①
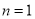 ,
, ,其中
,其中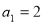 ,所以
,所以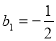 11分
11分
当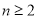 时,
时,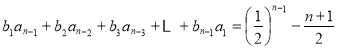 ②12分
②12分
②式两边同时乘以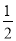 得,
得,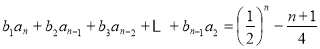 ③13分
③13分
①式减去③得,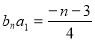 ,所以
,所以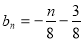 14分
14分
且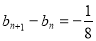 15分
15分
所以数列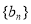 是以
是以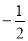 为首项,公差为
为首项,公差为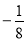 的等差数列。16分.
的等差数列。16分.
考点:1.数列的递推关系;2.等比数列的性质;2.数列求和,

练习册系列答案
相关题目
 (B)
(B) (C)
(C) (D)
(D)
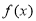 为定义在
为定义在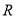 上的奇函数,当
上的奇函数,当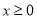 时,
时,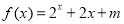 (
(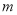 为常数),则
为常数),则 
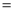 ( )
( )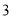 B.
B.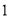 C.
C.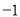 D.
D.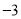
 中,三个内角
中,三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,
, ,
,  ,则
,则 .
. 的单调递增区间是 .
的单调递增区间是 .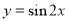 的图像,只需将函数
的图像,只需将函数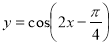 的图像( )
的图像( )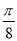 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向右平移
个单位 D.向右平移 (
( )的焦点在圆
)的焦点在圆 内,则实数
内,则实数 的取值范围是 .
的取值范围是 .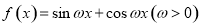 的最小正周期为
的最小正周期为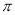 ,将
,将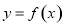 的图象向左平移
的图象向左平移 个单位得函数
个单位得函数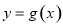 的图象,则
的图象,则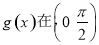 上单调递减
上单调递减 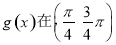 上单调递减
上单调递减 的解集是 .
的解集是 .