题目内容
已知圆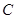
的参数方程为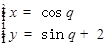
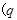为参数)，以原点为极点，
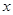轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为
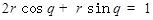, 则直线被圆所截得的弦长是 .
【答案】
【解析】
试题分析：∵
，∴圆C的方程为
，又直线的极坐标方程为
,∴直线的方程为2x+y-1="0," ∵圆心(0,2)到直线2x+y-1=0的距离为
，∴直线被圆所截得的弦长是
考点：本题考查了极坐标、参数方程与普通方程的互化及直线与圆的位置关系
点评：熟练掌握极坐标、参数方程与普通方程的互化及直线与圆的位置关系是解决此类问题的关键，属基础题
练习册系列答案
相关题目
已知圆的参数方程
（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线的极坐标方程为3ρcosα-4ρsinα-9=0，则直线与圆的位置关系是（ ）
|
| A、相切 | B、相离 |
| C、直线过圆心 | D、相交但直线不过圆心 |
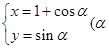为参数），直线
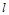的极坐标方程为
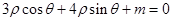，若圆与直线相切，则实数
________
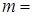为参数），以坐标原点为极点，
轴的正半轴
，则直线与圆的位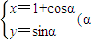
为参数），直线l的极坐标方程为3ρcosθ+4ρsinθ+m=0，若圆与直线相切，则实数m= ．