题目内容
已知椭圆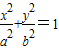 (a>b>0),离心率为
(a>b>0),离心率为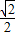 的椭圆经过点(
的椭圆经过点(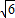 ,1).
,1).(1)求该椭圆的标准方程;
(2)过椭圆的一个焦点且互相垂直的直线l1,l2分别与椭圆交于A,B和C,D,是否存在常数λ,使得|AB|+|CD|=λ|AB|•|CD|?若存在,求出实数λ的值;若不存在,请说明理由.
【答案】分析:(1)由椭圆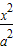 +
+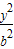 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=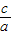 =
=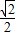 ,经过点(
,经过点(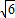 ,1)即
,1)即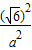 +
+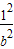 =1可求得a2,b2;
=1可求得a2,b2;
(2)设出直线AB,CD的方程与椭圆方程联立,求得相应弦长,利用|AB|+|CD|=λ|AB|•|CD|,可Q求得λ,从而问题得到解决.
解答:解:(1)∵椭圆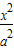 +
+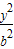 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为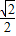 ,经过点(
,经过点(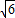 ,1),
,1),
∴e=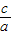 =
=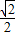 ?
?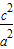 =
=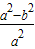 =
= ①,
①,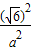 +
+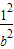 =1②,
=1②,
由①②解得a2=8,b2=4,
∴该椭圆的标准方程为: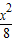 +
+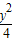 =1;
=1;
(2)∵椭圆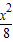 +
+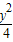 =1的左焦点F1(-2,0);
=1的左焦点F1(-2,0);
设过其左焦点F1的直线AB的方程为:y=k1(x+2),k1≠0
由方程组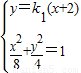 得(2
得(2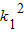 +1)x2+8
+1)x2+8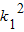 x+8
x+8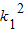 -8=0,
-8=0,
设A(x1,y1),B(x2,y2),则x1+x2=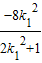 ,x1•x2=
,x1•x2=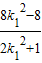
由弦长公式得|AB|=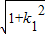 •
•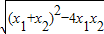 =
=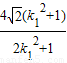 ,
,
同理设C(x3,y3),D(x4,y4),|CD|=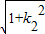 •
•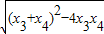 =
=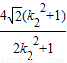 ,,
,,
由(1)k1•k2=-1得k2=-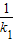 ,代入得|CD|=
,代入得|CD|=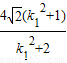 ,
,
∵|AB|+|CD|=λ|AB|•|CD|,
∴λ=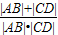 =
=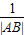 +
+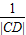 =
=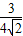 =
=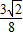 ,则存在λ=
,则存在λ=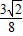 ,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
点评:本题重点考查直线与圆锥曲线的综合,解题的关键是直线与椭圆方程联立,利用弦长公式,综合性强,属于难题.
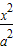 +
+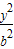 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=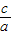 =
=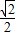 ,经过点(
,经过点(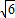 ,1)即
,1)即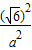 +
+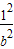 =1可求得a2,b2;
=1可求得a2,b2;(2)设出直线AB,CD的方程与椭圆方程联立,求得相应弦长,利用|AB|+|CD|=λ|AB|•|CD|,可Q求得λ,从而问题得到解决.
解答:解:(1)∵椭圆
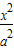 +
+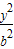 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为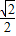 ,经过点(
,经过点(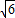 ,1),
,1),∴e=
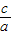 =
=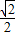 ?
?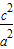 =
=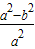 =
= ①,
①,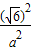 +
+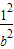 =1②,
=1②,由①②解得a2=8,b2=4,
∴该椭圆的标准方程为:
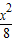 +
+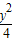 =1;
=1;(2)∵椭圆
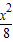 +
+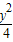 =1的左焦点F1(-2,0);
=1的左焦点F1(-2,0);设过其左焦点F1的直线AB的方程为:y=k1(x+2),k1≠0
由方程组
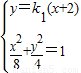 得(2
得(2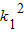 +1)x2+8
+1)x2+8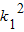 x+8
x+8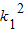 -8=0,
-8=0,设A(x1,y1),B(x2,y2),则x1+x2=
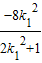 ,x1•x2=
,x1•x2=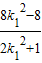
由弦长公式得|AB|=
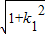 •
•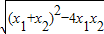 =
=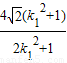 ,
,同理设C(x3,y3),D(x4,y4),|CD|=
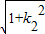 •
•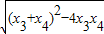 =
=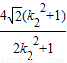 ,,
,,由(1)k1•k2=-1得k2=-
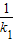 ,代入得|CD|=
,代入得|CD|=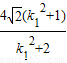 ,
,∵|AB|+|CD|=λ|AB|•|CD|,
∴λ=
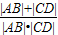 =
=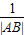 +
+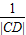 =
=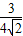 =
=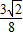 ,则存在λ=
,则存在λ=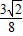 ,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
,使得|AB|+|CD|=λ|AB|•|CD|恒成立.点评:本题重点考查直线与圆锥曲线的综合,解题的关键是直线与椭圆方程联立,利用弦长公式,综合性强,属于难题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.