题目内容
已知:函数f(x)=2 sin
sin cos
cos -
-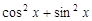
(1)求函数f( )的最小正周期;
)的最小正周期;
(2)当 ∈[0,
∈[0,  ]时,求f(x)的值域.
]时,求f(x)的值域.
 sin
sin cos
cos -
-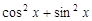
(1)求函数f(
 )的最小正周期;
)的最小正周期;(2)当
 ∈[0,
∈[0,  ]时,求f(x)的值域.
]时,求f(x)的值域.(1)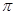 ;(2)[-1, 2].
;(2)[-1, 2].
 ;(2)[-1, 2].
;(2)[-1, 2].解决本题的关键是先把f(x)转化为f(x)=2sin(2x-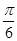 ),然后再考虑研究其单调性最值等.
),然后再考虑研究其单调性最值等.
解:f(x)= sin2x-(cos2x-sin2x)
sin2x-(cos2x-sin2x)
= sin2x-cos2x
sin2x-cos2x
=2(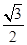 sin2x-
sin2x-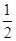 cos2x)
cos2x)
=2sin(2x-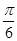 ) …………………………6分
) …………………………6分
(1)T=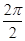 =
=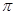 …………………………10分
…………………………10分
(2)0≤x≤ 0≤2x≤π
0≤2x≤π
-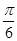 ≤2x-
≤2x-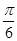 ≤
≤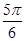
-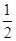 ≤sin(2x-
≤sin(2x- 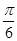 )≤1
)≤1
-1≤2sin(2x-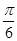 )≤2
)≤2
∴x∈[0, ]时,f(x)的值域为[-1, 2] …………………………16分
]时,f(x)的值域为[-1, 2] …………………………16分
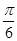 ),然后再考虑研究其单调性最值等.
),然后再考虑研究其单调性最值等.解:f(x)=
 sin2x-(cos2x-sin2x)
sin2x-(cos2x-sin2x)=
 sin2x-cos2x
sin2x-cos2x=2(
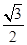 sin2x-
sin2x-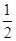 cos2x)
cos2x)=2sin(2x-
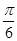 ) …………………………6分
) …………………………6分(1)T=
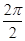 =
=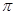 …………………………10分
…………………………10分(2)0≤x≤
 0≤2x≤π
0≤2x≤π-
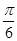 ≤2x-
≤2x-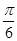 ≤
≤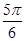
-
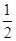 ≤sin(2x-
≤sin(2x- 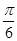 )≤1
)≤1 -1≤2sin(2x-
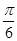 )≤2
)≤2∴x∈[0,
 ]时,f(x)的值域为[-1, 2] …………………………16分
]时,f(x)的值域为[-1, 2] …………………………16分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象向左平移
的图象向左平移 个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为
个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为 ,则( )
,则( )



 ,且
,且 是第二象限角,求
是第二象限角,求 的值。
的值。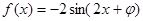 ,
, ,若
,若 对任意的
对任意的 恒成立,则
恒成立,则
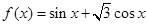
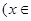 R
R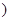 .
.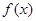 的最小正周期;
的最小正周期; ,
, ,
, ,且
,且 为锐角。
为锐角。 的值域。
的值域。 )
)  )
)
 的定义域是___________________________
的定义域是___________________________ cos
cos ,且
,且 ,则cos
,则cos 的值( )
的值( )
