题目内容
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为线段DD1,BD的中点.
(1)求三棱锥E-ADF的体积;
(2)求异面直线EF与BC所成的角.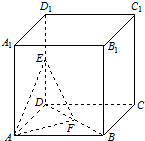
(1)求三棱锥E-ADF的体积;
(2)求异面直线EF与BC所成的角.

(1)∵正方体ABCD-A1B1C1D1棱长为2,E为线段DD1的中点.
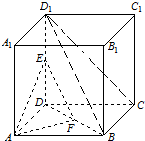
∴DE⊥平面ADF,且DE=1为三棱锥E-ADF的高
∵F是BD的中点
∴△ADF的面积S=
S△ABD=
SABCD=1
因此,三棱锥E-ADF的体积为V=
×S△ADF×DE=
×1×1=
(2)连接BC1、BD1
∵EF是△BDD1的中位线,
∴EF∥BD1,可得∠CBD1(或其补角)就是异面直线EF与BC所成的角.
∵BC⊥平面C1D1DC,CD1?平面C1D1DC,
∴Rt△BCD1中,tan∠CBD1=
=
=
可得∠CBD1=arctan
(锐角)
因此,异面直线EF与BC所成的角等于arctan
.

∴DE⊥平面ADF,且DE=1为三棱锥E-ADF的高
∵F是BD的中点
∴△ADF的面积S=
| 1 |
| 2 |
| 1 |
| 4 |
因此,三棱锥E-ADF的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)连接BC1、BD1
∵EF是△BDD1的中位线,
∴EF∥BD1,可得∠CBD1(或其补角)就是异面直线EF与BC所成的角.
∵BC⊥平面C1D1DC,CD1?平面C1D1DC,
∴Rt△BCD1中,tan∠CBD1=
| CD1 |
| BC |
2
| ||
| 2 |
| 2 |
可得∠CBD1=arctan
| 2 |
因此,异面直线EF与BC所成的角等于arctan
| 2 |

练习册系列答案
相关题目
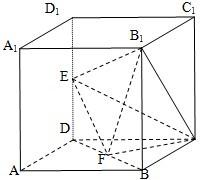 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.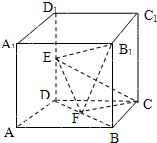 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点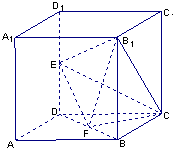 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 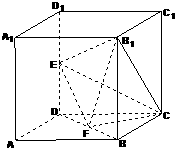 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.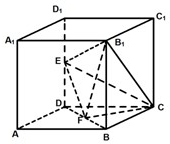 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.