题目内容

3．若直线y=kx与双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1无公共点，则实数k的取值范围是k≥$\frac{\sqrt{3}}{3}$或k≤-$\frac{\sqrt{3}}{3}$．

分析 将直线方程代入双曲线方程，化为关于x的方程，利用方程的判别式，即可求得k的取值范围．

解答 解：由题意，直线y=kx代入双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1，整理得（1-3k2）x2=6
∵y=kx与双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1无公共点，
∴1-3k2≤0，解得k≥$\frac{\sqrt{3}}{3}$或k≤-$\frac{\sqrt{3}}{3}$．
故答案为：k≥$\frac{\sqrt{3}}{3}$或k≤-$\frac{\sqrt{3}}{3}$．

点评 本题考查直线与圆锥曲线的关系，解题的关键是将两曲线有交点的问题转化为方程有根的问题，这是研究两曲线有交点的问题时常用的转化方向．

练习册系列答案
相关题目
13．已知双曲线与椭圆$\frac{x^2}{36}+\frac{y^2}{27}=1$有相同的焦点，且虚轴的长为4．
（Ⅰ）求双曲线的方程；
（Ⅱ）求双曲线的渐近线方程．
14．对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数．
（1）函数f1（x）=x2-x，f2（x）=x2+x+1，h（x）=x2-x+1，h（x）是否为f1（x），f2（x）的生成函数？说明理由；
（2）设f1（x）=1-x，f2（x）=$\frac{{{x^2}-x+1}}{x-1}$，当a=b=1时生成函数h（x），求h（x）的对称中心（不必证明）；
（3）设f1（x）=x，${f_2}（x）=\frac{1}{x-1}$（x≥2），取a=2，b＞0，生成函数h（x），若函数h（x）的最小值是5，求实数b的值．
11．设$a={log_{\frac{1}{2}}}3，b={（\frac{1}{2}）^{0.4}}，c={3^{\frac{1}{2}}}$则a，b，c的大小关系是（　　）
A．c＞b＞aB．c＞a＞bC．b＞a＞cD．a＞b＞c
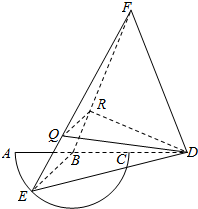18．如图，弧$\widehat{AEC}$是半径为a的半圆，AC为直径，点E为弧$\widehat{AC}$的中点，点B和点C为线段AD的三等分点，平面AEC外一点F满足FB=FD=$\sqrt{5}$a，FE=$\sqrt{6}$a．
（Ⅰ）证明：EB⊥FD；
（Ⅱ）已知点Q，R分别为线段FE，FB上的点，使得$\overrightarrow{FQ}$=λ$\overrightarrow{FE}$，$\overrightarrow{FR}$=λ$\overrightarrow{FB}$，求当RD最短时，平面BED与平面RQD所成二面角的正弦值．
8．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a、b∈R+）与x=3的一个交点P与两焦点的距离分别是$\frac{13}{2}$和$\frac{5}{2}$，求a与b的值．
15．已知圆：（x-2）2+y2=3与双曲线：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1，（a＞0，b＞0）$的渐近线相切，则双曲线的离心率为（　　）
A．$\frac{{2\sqrt{3}}}{3}$B．$\frac{4}{3}$C．2D．4
12．已知极坐标方程ρ=2cos（θ+$\frac{π}{3}$）和ρ=2cos（θ-$\frac{π}{3}$），求它的直角坐标方程，并求与之都外切的圆的圆心的轨迹方程．
13．已知递增的等差数列{an}的前三项和为6，前三项的积为6．
（Ⅰ）求等差数列{an}的通项公式；
（Ⅱ）设等差数列{an}的前n项和为Sn．记${b_n}=\frac{1}{S_n}$，求数列{bn}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网