题目内容
已知
且
，则
的最小值为
| A．1 | B．2 | C．4 | D．8 |
C
解析试题分析：因为根据题意可知
，又因为
两边平方可知
，当且仅当a=b=2时，取得最小值，故选C.
考点：本题主要考查均值不等式的求解最值的运用。
点评：解决该试题的关键是理解和为定值，则可通分合并得
结合
,可知a+b的最小值问题。
练习册系列答案
相关题目
若
且
，则下列不等式恒成立的是
A． | B． | C． | D． |
已知
则
的最小值为（ ）
A． | B． | C． | D． |
已知
，则
的最小值是（ ）
A． | B． | C． | D．5 |
已知
，
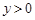，且
，则
的最小值是 （ ）
A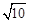． | B． | C． | D． |
已知函数
（
，且
）的图象恒过定点，若点在一次函数
的图象上，其中
，则
的最小值为（ ）
| A．4 | B． | C．2 | D．1 |
若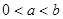
，且
，则在下列四个选项中，最大的是( )
A． | B． | C． | D． |
下列不等式一定成立的是（ ）
A． | B． |
C． | D． |
，2)，其横截距与纵截距分别为a、b(a、b均为正数)，则使a＋b≥c恒成立的c的取值范围为________．