题目内容
已知函数 (
( ,且
,且 )的图象恒过定点,若点在一次函数
)的图象恒过定点,若点在一次函数 的图象上,其中
的图象上,其中 ,则
,则 的最小值为( )
的最小值为( )
| A.4 | B. | C.2 | D.1 |
A
解析试题分析:根据指数函数的性质,可以求出A点,把A点代入一次函数y=mx+n,得出m+n=1,然后利用不等式的性质进行求解.
∵函数y=ax-1(a>0,且a≠1)的图象恒过定点A,可得A(1,1),∵点A在一次函数y=mx+n的图象上,∴m+n=1,∵m,n>0,∴m+n=1≥2 ,∴mn≤
,∴mn≤ ,所以
,所以 ,当且仅当n=m=1时取得等号。故选A.
,当且仅当n=m=1时取得等号。故选A.
考点:本试题主要考查了的指数函数和一次函数的性质及其应用,还考查的均值不等式的性质,把不等式和函数联系起来进行出题,是一种常见的题型。
点评:解决该试题的关键找到指数函数必定过(0,1)点得到已知函数过点(1,1)

练习册系列答案
相关题目
已知正数 满足
满足 则
则 的最小值为( )
的最小值为( )
A. | B.4 | C. | D. |
若a <0,则a + ( )
( )
| A.有最小值2 | B.有最大值2 |
| C.有最小值-2 | D.有最大值-2 |
若三点 (2,2),
(2,2),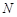 (
( ,0),
,0), (0,
(0,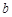 ),(
),( )共线,则
)共线,则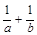 的值为( )
的值为( )
| A.1 | B. | C. | D. |
已知 且
且 ,则
,则 的最小值为
的最小值为
| A.1 | B.2 | C.4 | D.8 |
若 ,则
,则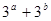 的最小值( )
的最小值( )
| A.4 | B.5 | C.6 | D.7 |
已知正实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
| A.2 | B. | C.3 | D. |
 则函数
则函数 的最大值为
的最大值为  满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) B
B  C
C  D
D 