题目内容
证明：对于任意实数t，复数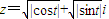
的模r=|z|适合
．
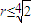【答案】分析：先求出复数z的模，利用分析法证明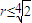
即可．
解答：证明：复数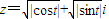
（其中t是实数）的模r=|z|为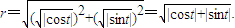
要证对任意实数t，有
，
只要证对任意实数t，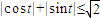
成立
对任意实数t，因为|cost|2+|sint|2=1
所以可令cosϕ=|cost|，sinϕ=|sint|，
且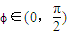
，
于是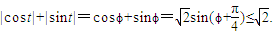
点评：本题考查复数的模，三角函数的基本关系式，是中档题．
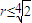即可．解答：证明：复数
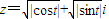（其中t是实数）的模r=|z|为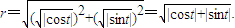要证对任意实数t，有
，只要证对任意实数t，
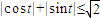成立对任意实数t，因为|cost|2+|sint|2=1
所以可令cosϕ=|cost|，sinϕ=|sint|，
且
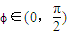，于是
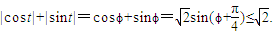
点评：本题考查复数的模，三角函数的基本关系式，是中档题．
练习册系列答案
阅读快车系列答案
相关题目