题目内容
17.求函数y=3sin($\frac{π}{4}$-2x)的单调区间,最小正周期、对称轴、对称中心,最小值及相应的x值.分析 由条件利用正弦函数的周期性、单调性、最值,以及正弦函数的图象的对称性,得出结论.
解答 解:函数y=3sin($\frac{π}{4}$-2x)=-3sin(2x-$\frac{π}{4}$)的最小正周期为$\frac{2π}{2}$=π.
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得 kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,可得函数的减区间为[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$],k∈Z;
令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,求得 kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,可得函数的增区间为[kπ+$\frac{3π}{8}$,kπ+$\frac{7π}{8}$],k∈Z.
令2x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{3π}{8}$,可得函数的图象的对称轴方程为 x=$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z.
令2x-$\frac{π}{4}$=kπ,求得x=$\frac{kπ}{2}$+$\frac{π}{8}$,可得函数的图象的对称中心为 ($\frac{kπ}{2}$+$\frac{π}{8}$,0),k∈Z.
令2x-$\frac{π}{4}$=2kπ+$\frac{π}{2}$,求得x=kπ+$\frac{3π}{8}$,可得当x=kπ+$\frac{3π}{8}$,k∈Z时,函数y取得最小值为-3.
点评 本题主要考查正弦函数的周期性、单调性、最值,以及正弦函数的图象的对称性,属于基础题.

| A. | (1,4) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
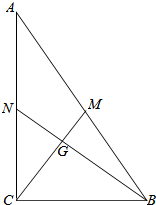 如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.
如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长. 如图所示,已知菱形ABCD,∠B=60°,现以AB为轴,菱形ABCD绕AB旋转一周,画出几何体的大致形状,并指明它是由哪些简单几何体组成?
如图所示,已知菱形ABCD,∠B=60°,现以AB为轴,菱形ABCD绕AB旋转一周,画出几何体的大致形状,并指明它是由哪些简单几何体组成?