题目内容
设函数 (x>0),则y=f(x) (
)
(x>0),则y=f(x) (
)
A.在区间 ,(1,e)内均有零点
,(1,e)内均有零点
B.在区间 ,(1,e)内均无零点
,(1,e)内均无零点
C.在区间 内有零点,在区间(1,e)内无零点
内有零点,在区间(1,e)内无零点
D.在区间 内无零点,在区间(1,e)内有零点
内无零点,在区间(1,e)内有零点
【答案】
:D
【解析】: ,导函数为
,导函数为 ,函数在(0,3)上为减函数,
,函数在(0,3)上为减函数, ,因此在区间
,因此在区间 内无零点,在区间(1,e)内有零点
内无零点,在区间(1,e)内有零点

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知函数 ,
, .
.
(Ⅰ)若函数 和函数
和函数 在区间
在区间 上均为增函数,求实数
上均为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有唯一解,求实数
有唯一解,求实数 的值.
的值.
【解析】第一问, 
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数
上均为增函数
(Ⅱ)中方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解得到结论。
有唯一解得到结论。
(Ⅰ)解:
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数 ……………6分
上均为增函数 ……………6分
(Ⅱ)方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解
有唯一解
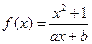 是其定义域内的奇函数,且
是其定义域内的奇函数,且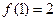
 18
18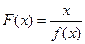 (x > 0 )
(x > 0 )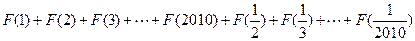 的值.
的值.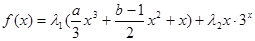
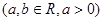 .
.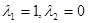 ,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证:
,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证: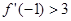 ;
;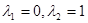 时,
时,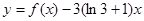 (x>0)的最小值;
(x>0)的最小值;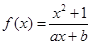 是其定义域内的奇函数,且
是其定义域内的奇函数,且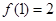
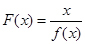 ( x > 0 )
( x > 0 ) 的值.
的值.





