题目内容
6.数列{an}为等差数列,3a8=5a13,前n项和为Sn.(1)若a1=39,求an.
(2)若a1>0,求Sn最大时n的值.
分析 (1)通过3a8=5a13及a1=39,计算即得结论;
(2)通过(1)得2a1=-39d,利用an=a1+(n-1)d>0,计算即可.
解答 解:(1)∵3a8=5a13,
∴3(a1+7d)=5(a1+12d)(d为公差),
即3a1+21d=5a1+60d,
又a1=39,解得d=-2,
∴an=a1+(n-1)d=41-2n;
(2)由(1)得2a1=-39d,
又令an=a1+(n-1)d>0得,$\left.\begin{array}{l}{a_1}+({n-1})\frac{{-2{a_1}}}{39}>0\\{a_1}>0\end{array}\right\}⇒n<\frac{41}{2}$,
即an>0?n=1,2,…,20,
an<0?n≥21,
∴当Sn最大时,n=20.
点评 本题考查求等差数列的通项及和的最大值,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.函数$y=cos(x+\frac{π}{12})$的图象的一条对称轴的方程是( )
| A. | $x=\frac{5π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{12}$ | D. | x=-$\frac{π}{12}$ |
1.先将函数y=sin2x的图象向右平移$\frac{π}{3}$个单位长度,再作所得的图象关于y轴的对称图形,则最后函数图象的解析式为( )
| A. | $y=sin(-2x-\frac{2π}{3})$ | B. | $y=sin(-2x+\frac{2π}{3})$ | C. | $y=sin(-2x-\frac{π}{3})$ | D. | $y=sin(-2x+\frac{π}{3})$ |
11.袋中有3个黑球7个红球,从中任取3个,以下选项可以作为随机变量的是( )
| A. | 取到的球的个数 | B. | 取到红球的个数 | ||
| C. | 至少取到一个红球 | D. | 至少取到一个红球的概率 |
16.如图所示的程序框图的运行结果是( )
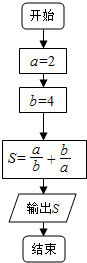

| A. | 2 | B. | 2.5 | C. | 3.5 | D. | 4 |