题目内容
已知向量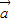 =(sinx,
=(sinx, ),
),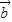 =(cosx,-1).
=(cosx,-1).(1)当
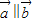 时,求cos2x-sin2x的值;
时,求cos2x-sin2x的值;(2)设函数f(x)=2(
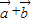 )-
)-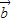 ,已知在△ABC中,内角A、B、C的对边分别为a、b、c,若a=
,已知在△ABC中,内角A、B、C的对边分别为a、b、c,若a=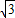 ,b=2,sinB=
,b=2,sinB=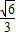 ,求 f(x)+4cos(2A+
,求 f(x)+4cos(2A+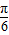 )(x∈[0,
)(x∈[0,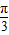 ])的取值范围.
])的取值范围.
【答案】分析:(1)由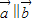 可得
可得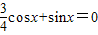 ,从而可求tanx,而
,从而可求tanx,而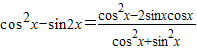
(2)由正弦定理得, 可求A=
可求A=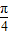 代入可得
代入可得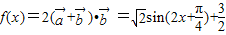 ,结合已知x
,结合已知x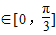 可求函数的值域
可求函数的值域
解答:解:(1)∵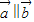
∴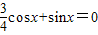
∴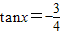 (2分)
(2分)
 (6分)
(6分)
(2)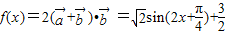
由正弦定理得,
所以A=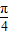 (9分)
(9分)
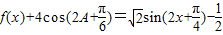
∵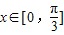 ∴
∴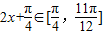
所以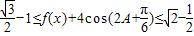 (12分)
(12分)
点评:本题主要考查了向量平行的坐标表示,利用1=sin2x+cos2x的代换,求解含有sinx,cosx的齐次式,向量的数量积的坐标表示,三角函数在闭区间上的值域的求解.
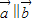 可得
可得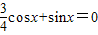 ,从而可求tanx,而
,从而可求tanx,而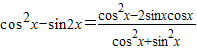
(2)由正弦定理得,
 可求A=
可求A=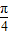 代入可得
代入可得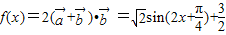 ,结合已知x
,结合已知x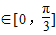 可求函数的值域
可求函数的值域解答:解:(1)∵
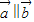
∴
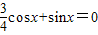
∴
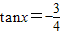 (2分)
(2分) (6分)
(6分)(2)
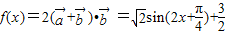
由正弦定理得,

所以A=
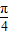 (9分)
(9分)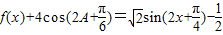
∵
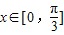 ∴
∴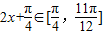
所以
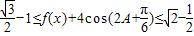 (12分)
(12分)点评:本题主要考查了向量平行的坐标表示,利用1=sin2x+cos2x的代换,求解含有sinx,cosx的齐次式,向量的数量积的坐标表示,三角函数在闭区间上的值域的求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(sinx,cosx),向量
=(1,
),则|
+
|的最大值为( )
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |