��Ŀ����
1�����M��x��y�����㲻��ʽ��$\left\{\begin{array}{l}{3x-y-6��0}\\{x-y+2��0}\\{x��0��y��0}\end{array}\right.$����P��$\frac{1}{a}$��$\frac{1}{b}$����a��0��b��0������$\overrightarrow{OP}$•$\overrightarrow{OM}$���ʱ����MΪ��������| A�� | ��0��2�� | B�� | ��0��0�� | C�� | ��4��6�� | D�� | ��2��0�� |
���� ��������ƽ�����Ӷ�����$\overrightarrow{OP}$•$\overrightarrow{OM}$=��$\frac{1}{a}$��$\frac{1}{b}$��•��x��y��=$\frac{x}{a}$+$\frac{y}{b}$���Ӷ�ȷ�����ֵʱ�ĵ㼴�ɣ�
��� �⣺��������ƽ���������£�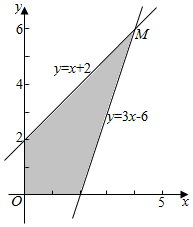 ��
��
$\overrightarrow{OP}$•$\overrightarrow{OM}$=��$\frac{1}{a}$��$\frac{1}{b}$��•��x��y��=$\frac{x}{a}$+$\frac{y}{b}$��
�ʵ�x��y�������ֵʱ��
��x=4��y=6ʱ�������ֵ��
��ѡC��
���� ���⿼�������Թ滮�Ľⷨ�����ν�ϵ�˼�뷽��Ӧ�ã������е��⣮

��ϰ��ϵ�д�
 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
�����Ŀ
9����֪˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0�������Ҷ���ֱ�ΪA��B������Ķ˵�����ԭ��ΪԲ�ģ�|AB|Ϊֱ����Բ�ϣ�PΪ��˫������һ�㣬��ֱ��PB��б��Ϊ$\sqrt{2}$����ֱ��PA��б��Ϊ��������
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | $\frac{\sqrt{3}}{2}$ |
16������f��x��=Asin��x+�գ���A��0����x=$\frac{��}{3}$��ȡ����Сֵ��������
| A�� | f��x+$\frac{��}{3}$�����溯�� | B�� | f��x+$\frac{��}{3}$����ż���� | C�� | f��x-$\frac{��}{3}$�����溯�� | D�� | f��x-$\frac{��}{3}$����ż���� |
13������{an}��ͨ�ʽΪan=2n-1����ǰn���Sn=��������
| A�� | n2-1 | B�� | n2 | C�� | n2+1 | D�� | ��n+1��2 |
3����ֱ�������У���ACB=90�㣬AC=BC=1������AA1=$\sqrt{2}$��MΪA1B1���е㣬��AM��ƽ��AA1C1C���ɽǵ�����ֵΪ��������
| A�� | $\frac{1}{3}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{\sqrt{2}}{3}$ | D�� | $\frac{2}{3}$ |