题目内容
如图，在四面体OABC中，G是底面△ABC的重心，则
等于（ ）
| OG |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
分析：利用重心的性质和向量的三角形法则即可得出．
解答：解：如图所示，连接AG并延长与BC相交于点D．
∵点G是底面△ABC的重心，
∴
=
，
=
(
+
)．
∴
=
+
=
+
×
(
+
)
=
+
(
+
)．
又
=
-
，
=
-
，
∴
=
+
(
-
+
-
)
=
(
+
+
)．
故选：D．
∵点G是底面△ABC的重心，
∴
| AG |
| 2 |
| 3 |
| AD |
| AD |
| 1 |
| 2 |
| AB |
| AC |
∴
| OG |
| OA |
| AG |
| OA |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
=
| OA |
| 1 |
| 3 |
| AB |
| AC |
又
| AB |
| OB |
| OA |
| AC |
| OC |
| OA |
∴
| OG |
| OA |
| 1 |
| 3 |
| OB |
| OA |
| OC |
| OA |
=
| 1 |
| 3 |
| OA |
| OB |
| OC |
故选：D．
点评：本题考查了重心的性质和向量的三角形法则，属于基础题．
练习册系列答案
相关题目
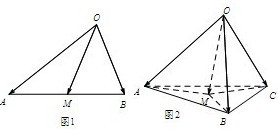如图1，在△OAB中，M是AB边上的点，则
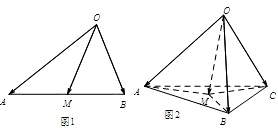如图1，在△OAB中，M是AB边上的点，则
=
+
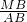
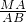
，类比到空间向量，如图2，在四面体OABC中，M是△ABC内一点，那么下列结论正确的是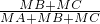
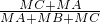
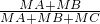
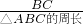
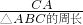
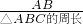
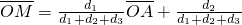
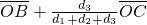（其中d1、d2、d3分别表示M到BC、CA、AB的距离）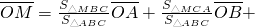
=
+
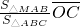
，类比到空间向量，如图2，在四面体OABC中，M是△ABC内一点，那么下列结论正确的是（ ）
=
+
+
=
+
+
（其中d1、d2、d3分别表示M到BC、CA、AB的距离）
