题目内容
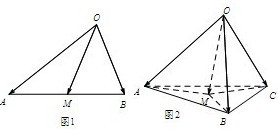 如图1,在△OAB中,M是AB边上的点,则
如图1,在△OAB中,M是AB边上的点,则| OM |
| MB |
| AB |
| OA |
| MA |
| AB |
| OB |
分析:从平面的结论推广到空间,线段长的比类比到面积的比值,因此可以类似地写出四面体OABC中
关于
、
、
的线性组合形式,再用平面几何结合向量的有关知识加以证明,即可得到本题答案.
| OM |
| OA |
| OB |
| OC |
解答:解: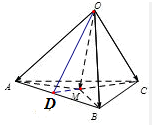 根据平面内的结论:在△OAB中,M是AB边上的点,则
根据平面内的结论:在△OAB中,M是AB边上的点,则
=
+
,
推广到空间:在四面体OABC中,M是△ABC内一点,
则
=
+
+
.证明如下:
延长CM,交AB于D,连接OD,可得
=
+
,
=
+
∴
=
+
(
+
)
∵
=
,
•
=
,
•
=
∴
=
+
+
故选:D
 根据平面内的结论:在△OAB中,M是AB边上的点,则
根据平面内的结论:在△OAB中,M是AB边上的点,则| OM |
| MB |
| AB |
| OA |
| MA |
| AB |
| OB |
推广到空间:在四面体OABC中,M是△ABC内一点,
则
. |
| OM |
| S△MBC |
| S△ABC |
. |
| OA |
| S△MCB |
| S△ABC |
. |
| OB |
| S△MAB |
| S△ABC |
. |
| OC |
延长CM,交AB于D,连接OD,可得
| OM |
| DM |
| DC |
| OC |
| CM |
| DC |
| OD |
| OD |
| AD |
| AB |
| OB |
| BD |
| AB |
| OA |
∴
| OM |
| DM |
| DC |
| OC |
| CM |
| DC |
| AD |
| AB |
| OB |
| BD |
| AB |
| OA |
∵
| DM |
| DC |
| S△MAB |
| S△ABC |
| CM |
| DC |
| AD |
| AB |
| S△MCA |
| S△ABC |
| CM |
| DC |
| BD |
| AB |
| S△MBC |
| S△ABC |
∴
| OM |
| S△MBC |
| S△ABC |
| OA |
| S△MCA |
| S△ABC |
| OB |
| S△MAB |
| S△ABC |
. |
| OC |
故选:D
点评:本题给出平面向量的一个结论,要求将此结论类比到空间,着重考查了平面向量基本定理和进行简单的合情推理等知识,属于基础题.

练习册系列答案
相关题目
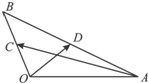 如图,在△OAB中,∠AOB=120°,OA=2,OB=1,C、D分别是线段OB和AB的中点,那么
如图,在△OAB中,∠AOB=120°,OA=2,OB=1,C、D分别是线段OB和AB的中点,那么| OD |
| AC |
| A、-2 | ||
B、-
| ||
C、-
| ||
D、
|
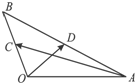 如图,在△OAB中,∠AOB=120°,OA=2,OB=1,C、D分别是线段OB和AB的中点,那么
如图,在△OAB中,∠AOB=120°,OA=2,OB=1,C、D分别是线段OB和AB的中点,那么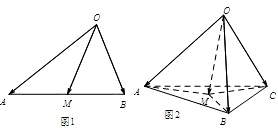 如图1,在△OAB中,M是AB边上的点,则
如图1,在△OAB中,M是AB边上的点,则 =
=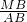
 +
+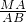
 ,类比到空间向量,如图2,在四面体OABC中,M是△ABC内一点,那么下列结论正确的是
,类比到空间向量,如图2,在四面体OABC中,M是△ABC内一点,那么下列结论正确的是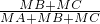
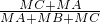
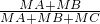

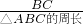
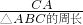
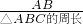
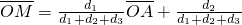
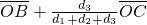 (其中d1、d2、d3分别表示M到BC、CA、AB的距离)
(其中d1、d2、d3分别表示M到BC、CA、AB的距离)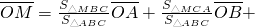
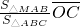
 =
=
 +
+
 ,类比到空间向量,如图2,在四面体OABC中,M是△ABC内一点,那么下列结论正确的是( )
,类比到空间向量,如图2,在四面体OABC中,M是△ABC内一点,那么下列结论正确的是( )
 =
=
 +
+
 +
+

 =
=
 +
+
 +
+


 (其中d1、d2、d3分别表示M到BC、CA、AB的距离)
(其中d1、d2、d3分别表示M到BC、CA、AB的距离)
