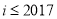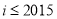题目内容
已知函数 ,
,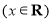 .
.
(1)证明:函数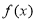 在区间
在区间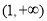 上为增函数,并指出函数
上为增函数,并指出函数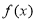 在区间
在区间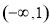 上的单调性.
上的单调性.
(2)若函数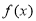 的图像与直线
的图像与直线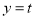 有两个不同的交点
有两个不同的交点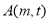 ,
, ,其中
,其中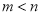 ,求
,求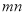 关于
关于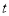 的函数关系式.
的函数关系式.
(3)求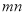 的取值范围.
的取值范围.
(1)见解析;(2)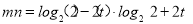 ;(3)
;(3)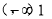 .
.
【解析】
试题分析:(1)用单调性的定义取值,做差,判断与零的关系,证明即可;(2)易知A(m,t),B(n,t)分别位于直线x=1的两侧,由m<n,得m<1<n,故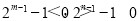 ,易得mn的表达式,解之即可;(3)分两种情况,当
,易得mn的表达式,解之即可;(3)分两种情况,当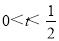 时,当
时,当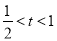 时,再由基本不等式可得.
时,再由基本不等式可得.
试题解析: (1)证明:任取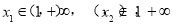 且
且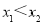
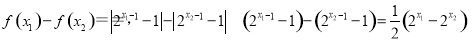
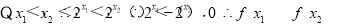
 所以f(x)在区间
所以f(x)在区间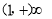 上为增函数.函数f(x)在区间
上为增函数.函数f(x)在区间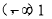 上为减函数.
上为减函数.
(2)因为函数f(x)在区间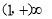 上为增函数,相应的函数值为
上为增函数,相应的函数值为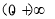 ,在区间
,在区间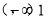 上为减函数,相应的函数值为(0,1),由题意函数f(x)的图象与直线y=t有两个不同的交点,故有t∈(0,1),易知A(m,t),B(n,t)分别位于直线x=1的两侧,
上为减函数,相应的函数值为(0,1),由题意函数f(x)的图象与直线y=t有两个不同的交点,故有t∈(0,1),易知A(m,t),B(n,t)分别位于直线x=1的两侧,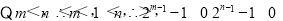
又A,B两点的坐标满足方程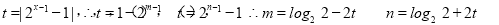
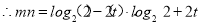
(3)当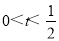 时,
时,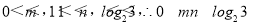
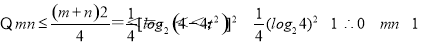
当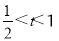 时,
时,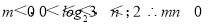 综上mn的取值范围为
综上mn的取值范围为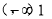 .
.
考点:函数的图象;函数单调性的性质.

练习册系列答案
相关题目
 是定义在R上的周期为3的函数,当
是定义在R上的周期为3的函数,当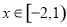 时,
时,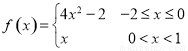 ,则
,则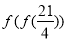 =( )
=( )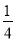 B.
B.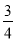 C.
C. D.0
D.0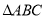 中,内角
中,内角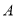 ,
,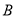 ,
,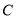 所对应的边分别为
所对应的边分别为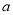 ,
, ,
,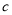 ,若
,若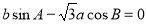 ,且
,且 ,则
,则 的值为( )
的值为( )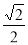 B.
B.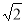 C.2 D.4
C.2 D.4 为单位向量,其中
为单位向量,其中 ,且
,且 在
在 上的投影为2,则
上的投影为2,则 与
与 的夹角
的夹角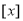 表示不超过
表示不超过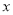 的最大整数),则输出的
的最大整数),则输出的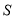 值为( )
值为( )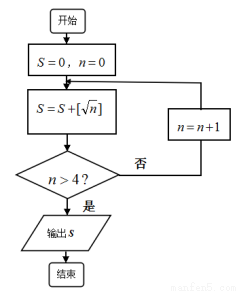
 的图象为( )
的图象为( ) B.
B. C.
C. D.
D.
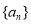 是以
是以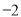 为公差的等差数列,
为公差的等差数列,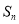 是其前
是其前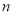 项和,若
项和,若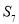 是数列
是数列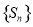 中的唯一最大项,则数列
中的唯一最大项,则数列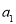 的取值范围是 .
的取值范围是 . 的图象为( )
的图象为( ) B.
B. C.
C. D.
D.
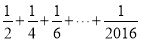 的值的程序框图,其中判断框内应填入的是( )
的值的程序框图,其中判断框内应填入的是( )