题目内容
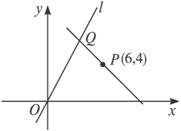
已知直线l:y=4x与点P(6,4),在l上求一点Q,使直线PQ与直线l,以及x轴在第一象限内围成的三角形面积最小.
解:设点Q(x0,4x0),①当x0=6时,PQ⊥x轴,S△=![]() ×6×4×6=72.
×6×4×6=72.
②当x0≠6时,∴直线PQ的倾斜角大于直线l的倾斜角.∴![]() >4或
>4或![]() <0.解得x0>6或1<x0<6.
<0.解得x0>6或1<x0<6.
直线PQ的方程:y-4=![]() (x-6).
(x-6).
令y=0,得x=![]() .
.
∴S△=![]() ·
·![]() ×4x0=
×4x0=![]() .
.
设x0-1=t,∵x0∈(1,6)∪(6,+∞),
∴t∈(0,5)∪(5,+∞).
∴S△=![]() =10(t+
=10(t+![]() +2)≥10×(2
+2)≥10×(2![]() +2)=40,40<72.
+2)=40,40<72.
∴S△的最小值=40.此时t=![]()
![]() t=1
t=1![]() x0=2.∴Q(2,8).
x0=2.∴Q(2,8).

练习册系列答案
相关题目
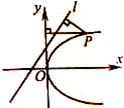 如图,已知直线l:4x-3y+6=0,抛物线C:y2=4x图象上的一个动点P到直线l与y轴的距离之和的最小值是
如图,已知直线l:4x-3y+6=0,抛物线C:y2=4x图象上的一个动点P到直线l与y轴的距离之和的最小值是