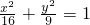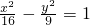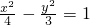题目内容
下列曲线方程满足横坐标范围是[-4,4]的是( )
分析:分别将曲线方程变形,利用一个数的平方大于等于0,建立不等式,从而可求出结论
解答:解:由
+
=1可得
=1 -
,∴1 -
≥0,∴-2≤x≤2,不满足题意;
由
+
=1可得
=1-
,∴1-
≥0,,∴-4≤x≤4,满足题意;
由
-
=1可得
=
-1,∴
-1≥0,∴x≤-4或x≥4,不满足题意;
由
-
=1可得
=
-1,∴
-1≥0,,∴x≤-2或x≥2,不满足题意;
故选B.
| x2 |
| 4 |
| y2 |
| 3 |
| y2 |
| 3 |
| x2 |
| 4 |
| x2 |
| 4 |
由
| x2 |
| 16 |
| y2 |
| 9 |
| y2 |
| 9 |
| x2 |
| 16 |
| x2 |
| 16 |
由
| x2 |
| 16 |
| y2 |
| 9 |
| y2 |
| 9 |
| x2 |
| 16 |
| x2 |
| 16 |
由
| x2 |
| 4 |
| y2 |
| 3 |
| y2 |
| 3 |
| x2 |
| 4 |
| x2 |
| 4 |
故选B.
点评:本题考查的重点是求参数的范围,解题的关键是利用一个数的平方大于等于0,建立不等式.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知两点M(1,
),N(-4,-
),给出下列曲线方程:
①4x+2y-1=0
②x2+y2=3
③
+y2=1
④
-y2=1
在曲线上存在P满足|MP|=|NP|的所有曲线方程是
| 5 |
| 4 |
| 5 |
| 4 |
①4x+2y-1=0
②x2+y2=3
③
| x2 |
| 2 |
④
| x2 |
| 2 |
在曲线上存在P满足|MP|=|NP|的所有曲线方程是
②③④
②③④
.